
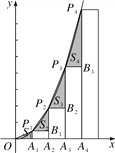
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图1,□OABC的边OC在y轴的正半轴上,OC=3,A(2,1),反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
(1)求点B的坐标和反比例函数的关系式;
(2)如图2,将线段OA延长交y=![]() (x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.
(x>0)的图象于点D,过B,D的直线分别交x轴、y轴于E,F两点,①求直线BD的解析式;②求线段ED的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的4 000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
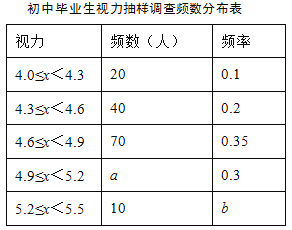
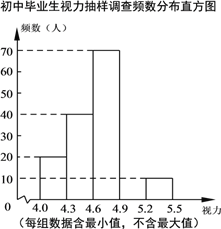
(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】彼此相似的矩形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
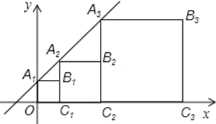
A. (2n﹣1,2n)B. (2n﹣![]() ,2n)
,2n)
C. (2n﹣1﹣![]() ,2n﹣1)D. (2n﹣1﹣1,2n﹣1)
,2n﹣1)D. (2n﹣1﹣1,2n﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
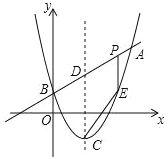
(1)求m的值和该二次函数的表达式.为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(3)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com