
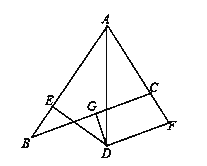
【题目】已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
⑴试说明:BE=CF;
⑵若AF=3,BC=4,求△ABC的周长.
【答案】(1)证明详见解析;(2)10.
【解析】试题分析:(1)连接DB、DC,根据角平分线性质和垂直平分线的性质得:DE=DF,DB=DC,证明Rt△BED≌Rt△CFD(HL),得出结论;
(2)先证明△AED≌△AFD,得AF=AE=3,再将△ABC的周长进行等量代换,即△ABC的周长=AB+AC+BC=AE+EB+AF﹣CF+BC,代入求值即可.
试题解析:连接DB、DC,
(1)∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵DG垂直平分BC,
∴DB=DC,
在Rt△BED和Rt△CFD中,
DE=DF,BD=CD,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)∵∠DAE=∠DAF,∠AED=∠AFD=90°,AD=AD,
∴△AED≌△AFD,
∴AF=AE=3,
由(1)得:BE=CF,
∴△ABC的周长=AB+AC+BC=AE+EB+AF﹣CF+BC=AE+AF+BC=3+3+4=10.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】已知海拔每升高1千米,温度下降6℃,某时刻A地底面温度为20℃,高出地面x千米处的温度为y℃,则y与x之间的函数关系为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)

查看答案和解析>>
科目:初中数学 来源: 题型:
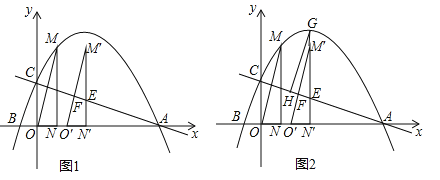
【题目】已知抛物线与x轴交于A(6,0)、B(![]() ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下面的日历,回答下列问题:
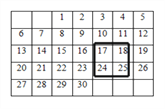
⑴在日历中,用正方形框圈出四个日期(如图),求出图中这四个数的和;
⑵任意用正方形框圈出四个日期,如果正方形
框中的第一个数为x,用代数式表示正方形框中
的四个数的和;
⑶若将正方形框上下左右移动,可框住另外的四个数,这四个数的和能等于40吗?如果能,依次写出这四个数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
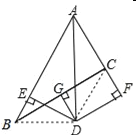
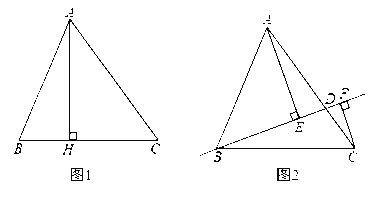
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com