Question

9．（1）操作发现：如图①，D是等边三角形ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边三角形DCF，连接AF．你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论．
（2）类比猜想：如图②，当动点D运动到等边三角形ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？如果成立，请证明；如果不成立，是否有新的结论？如果有新的结论，直接写出新的结论，不需证明．
（3）深入探究：
①如图③，当动点D在等边三角形ABC的边BA上运动时（点D与点B不重合），连接DC，以DC为边在其上方、下方分别作等边三角形DCF和等边三角形DCF'，连接AF，BF'．探究AF，BF'与AB有何数量关系？直接写出你的结论，不需证明．
②如图④，当动点D在等边三角形ABC的边BA的延长线上运动时，其他作法与图③相同，①中的结论是否仍然成立？如果成立，请证明；如果不成立，是否有新的结论？如果有新的结论，直接写出新的结论，不需证明．

Answer 1

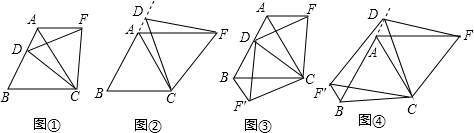
分析 （1）根据等边三角形的三条边、三个内角都相等的性质，利用全等三角形的判定定理SAS可以证得△BCD≌△ACF；然后由全等三角形的对应边相等知AF=BD；
（2）通过证明△BCD≌△ACF，即可证明AF=BD；
（3）①AF+BF′=AB；利用全等三角形△BCD≌△ACF（SAS）的对应边BD=AF；同理△BCF′≌△ACD（SAS），则BF′=AD，所以AF+BF′=AB；
②①中的结论不成立．新的结论是AF=AB+BF′；通过证明△BCF′≌△ACD（SAS），则BF′=AD（全等三角形的对应边相等）；再结合（2）中的结论即可证得AF=AB+BF′．

解答 解：（1）AF=BD；
证明如下：∵△ABC是等边三角形（已知），
∴BC=AC，∠BCA=60°（等边三角形的性质）；
同理知，DC=CF，∠DCF=60°；
∴∠BCA-∠DCA=∠DCF-∠DCA，即∠BCD=∠ACF；
在△BCD和△ACF中，
$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACF}\\{DC=FC}\end{array}\right.$，
∴△BCD≌△ACF（SAS），
∴BD=AF（全等三角形的对应边相等）；

（2）证明过程同（1），证得△BCD≌△ACF（SAS），则AF=BD（全等三角形的对应边相等），所以，当动点D运动至等边△ABC边BA的延长线上时，其他作法与（1）相同，AF=BD仍然成立；

（3）①AF+BF′=AB；
证明如下：由（1）知，△BCD≌△ACF（SAS），则BD=AF；
同理△BCF′≌△ACD（SAS），则BF′=AD，
∴AF+BF′=BD+AD=AB；

②、①中的结论不成立．新的结论是AF=AB+BF′；
证明如下：在△BCF′和△ACD中，
$\left\{\begin{array}{l}{BC=AC}\\{∠BCF′=∠ACD}\\{F′C=DC}\end{array}\right.$，
∴△BCF′≌△ACD（SAS），
∴BF′=AD（全等三角形的对应边相等）；
又由（2）知，AF=BD；
∴AF=BD=AB+AD=AB+BF′，即AF=AB+BF′．

点评 本题考查了三角形综合题．需要掌握全等三角形判定，全等三角形对应边相等的性质，本题中每一问都找出全等三角形并求证是解题的关键．