练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ）已知，如图，现有、的正方形纸片和的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．

    长为a＋2b，宽为a＋b   
     

    解析考点：作图—应用与设计作图．
    分析：面积为2a2+5ab+2b2，那么最小的正方形使用2次，较大的正方形使用2次，边长为a，b的长方形使用5次．
    解答：解：说明：答案不唯一，画图正确，不论画在什么位置，
    只要符合题意即可．不标出相应尺寸的扣（2分），标错1个或少标1个扣（1分）．

    点评：应根据题中所给的矩形的面积判断出各个图形使用的次数，进而进行拼合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

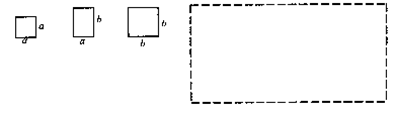
    科目：初中数学 来源： 题型：

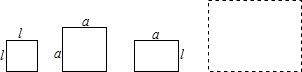
    3、已知，如图，现有a×a、b×b的正方形纸片和a×b的长方形纸片各若干块，试选用这些纸片（每种纸片至少用一次）拼成一个长方形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹，画出的图形尽可能跟原图一样标准），使拼出的长方形面积为2a2+5ab+2b2，并标出此长方形的长和宽．
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    观察下列方程和等式，寻找规律，完成问题：
    ①方程x2-7x+6=0，x1=1，x2=6，而x2-7x+6=（x-1）（x-6）；
    ②方程x2-4x-5=0，x1=5，x2=-1，而x2-4x-5=（x-5）（x+1）；
    ③方程4x2-12x+9=0，x1=
    3
    2
    ，x2=
    3
    2
    ，而4x2-12x+9=4(x-
    3
    2
    )(x-
    3
    2
    )    ；
    ④方程3x2+7x+4=0，x1=-
    4
    3
    ，x2=-1，而3x2+7x+4=3(x+
    4
    3
    )(x+1)    ；…
    （1）探究规律：当方程ax2+bx+c=0（a≠0）时，
     
    ；
    （2）解决问题：根据上述材料将下列多项式分解：x2-x-2；2x2+3x-2
    （3）拓广应用：已知，如图，现有1×1，a×a的正方形纸片和1×a的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为2a2+5a+2，并标出此矩形的长和宽．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    25、已知：如图①，现有a×a，b×b的正方形纸片和a×b的长方形纸片各若干块．

    （1）图②是用这些纸片拼成的一个长方形，（每两个纸片之间既不重叠，也无空隙），利用这个长方形的面积，写出一个代数恒等式
    （a+b）（a+2b）=a2+3ab+2b2
    ；
    （2）试选用图①中的纸片（每种纸片至少用一次）在下面的方框中拼成与图②不同的一个长方形，（拼出的图中必须保留拼图的痕迹），标出此长方形的长和宽，并利用拼成的长方形面积写出一个代数恒等式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．
    （1）求证：∠APB=∠BPH；
    （2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论．

    查看答案和解析>>

    同步练习册答案