
���� ��1�����M��N��ԭ��O�ľ��룬��С�ڻ����2ʱ���й����㣬��֮��û�У����ݹ����㶨�弴����⣻
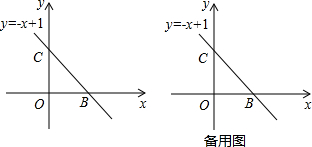
��2�������������y=-x+1�ϣ��ҵ�ԭ�������2�ĵ㣬�ݴ˼������m�ķ�Χ��
�ڷֳ�A��x�Ḻ�����x����������������������ۣ���õ��߶�BC�ϵ������2�ĵ㣬�ݴ˼�����⣮
��� �⣺��1����OM=1��2��
��M�й����㣬�������ǣ�-1��0����
��N�������ǣ�1��2����
��ON=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��2����Nû�й����㣻
��2���ٵ�x=mʱ��y=-m+1=1-m����P�������ǣ�m��1-m����
��OP=2ʱ��m2+��1-m��2=4��
��ã�m=$\frac{1��\sqrt{7}}{2}$��
��m��ȡֵ��Χ��$\frac{1-\sqrt{7}}{2}$��m��$\frac{1+\sqrt{7}}{2}$��
����y=-x+1�У���x=0�����y=1����C�������ǣ�0��1����
��y=0�����x=1����B�������ǣ�1��0����
��CD��BC����x���ڵ�D����CD=BC=$\sqrt{2}$��2��
��A��x��ĸ������ϣ���AC=2ʱ��OA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$��
��A��x����������ϣ�OB=1����OA=3��
��a�ķ�Χ��-$\sqrt{3}$��a��3��
���� ���⿼����һ�κ�����ͼ���������ۺ�Ӧ�ã����������������Ķ��壬��ȷ���з��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
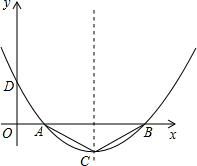 ��ͼ�����κ�����ͼ����D��0��$\frac{7}{9}\sqrt{3}$�����Ҷ���C�ĺ�����Ϊ4����ͼ����x���Ͻص��߶�AB��Ϊ6��
��ͼ�����κ�����ͼ����D��0��$\frac{7}{9}\sqrt{3}$�����Ҷ���C�ĺ�����Ϊ4����ͼ����x���Ͻص��߶�AB��Ϊ6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
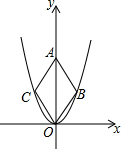 ��ͼ��O��B��C������ڶ��κ���y=$\sqrt{3}{x}^{2}$��ͼ���ϣ���OΪ����ԭ�㣬�ı���OBACΪ���Σ��ҡ�OBA=120�㣬��������OBAC�������
��ͼ��O��B��C������ڶ��κ���y=$\sqrt{3}{x}^{2}$��ͼ���ϣ���OΪ����ԭ�㣬�ı���OBACΪ���Σ��ҡ�OBA=120�㣬��������OBAC��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
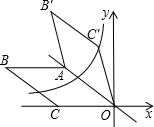 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A�������ǣ�-4��3��������C������Ϊ��-5��0����������OABC�ر�OA����ֱ�߷��ۣ��õ�����OAB��C�䣬������������y=$\frac{k}{x}$��x��0����ͼ��պþ�����C�䣬��k��ֵΪ$-\frac{168}{25}$��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A�������ǣ�-4��3��������C������Ϊ��-5��0����������OABC�ر�OA����ֱ�߷��ۣ��õ�����OAB��C�䣬������������y=$\frac{k}{x}$��x��0����ͼ��պþ�����C�䣬��k��ֵΪ$-\frac{168}{25}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
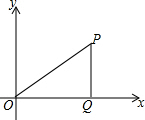 ��ͼ��ƽ��ֱ������ϵ��Rt��OPQ�Ķ���P������Ϊ��3��2��������OPQ��O����ʱ����ת90�����P������Ϊ��������
��ͼ��ƽ��ֱ������ϵ��Rt��OPQ�Ķ���P������Ϊ��3��2��������OPQ��O����ʱ����ת90�����P������Ϊ��������| A�� | ��-2��3�� | B�� | ��2��-3�� | C�� | ��3��2�� | D�� | ��-3��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com