
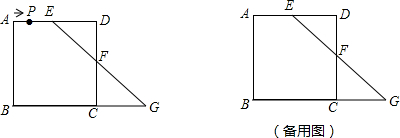
分析 (1)设FC=xcm,则EF=FC=xcm,DF=(40-x)cm,在直角△DEF中,利用勾股定理即可列方程求解;
(2)①以BC所在直线为x轴,AB所在直线为y轴建立坐标系,求得直线EF的解析式,根据P的横纵坐标相等即可求解;
②分成0<t≤4,4<t≤9,9<t≤$\frac{65}{4}$三种情况进行讨论,利用矩形的面积公式以及相似三角形的性质即可求解;
③根据②的结果列方程求解即可.
解答  解:(1)设FC=xcm,则EF=FC=xcm,DF=(40-x)cm.
解:(1)设FC=xcm,则EF=FC=xcm,DF=(40-x)cm.
在直角△DEF中,DE2+DF2=EF2,
则202+(40-x)2=x2,
解得:x=25,
则FC=25cm;
(2)①当P在AE上和FC上时,矩形PMBN不是正方形.
当P在EF上时,如图(1),如图建立坐标系,则E的坐标是(20,40),F的坐标是(40,25).
设EF的解析式是y=kx+b,
则$\left\{\begin{array}{l}{20k+b=40}\\{40k+b=25}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=55}\end{array}\right.$,
则直线EF的解析式是:y=-$\frac{3}{4}$x+55,
设P的坐标是(m,m),
代入y=-$\frac{3}{4}$x+55中得:m=-$\frac{3}{4}$m+55,
解得:m=$\frac{220}{7}$
则P的坐标是($\frac{220}{7}$,$\frac{220}{7}$);
则PE=$\sqrt{(\frac{220}{7}-20)^{2}+(\frac{220}{7}-40)^{2}}$=$\frac{100}{7}$.
则t=(20+$\frac{100}{7}$)÷5=$\frac{48}{7}$(s);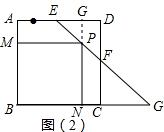
②当0<t≤4时,S=40t;
当4<t≤9时,P在EF上,如图(2),则PE=5t-20,作PG⊥AD于点G,
则△EGP∽△EDF,
则$\frac{GP}{DF}=\frac{EP}{EF}$=$\frac{EG}{ED}$,
∵直角△DEF中,EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25,
∴$\frac{GP}{15}$=$\frac{5t-20}{25}$=$\frac{EG}{20}$,
解得:GP=3t-12,EG=4t-16.
∴PN=40-GP=40-(3t-12)=52-3t,PM=40-DG=AE+EG=20+4t-16=4+4t,
则S=(52-3t)(4+4t)=-12t2+200t+208;
当9<t≤$\frac{65}{4}$时,P在FC上,N与C重合,PM=40,PN=5t-20-25=5t-45.
则S=40(5t-45)=200t-180.
即S=$\left\{\begin{array}{l}{40t(t≤4)}\\{-12{t}^{2}+200t+208(4<t≤9)}\\{200t-180(9<t≤\frac{65}{4})}\end{array}\right.$;
(3)当0<t≤4时,S的最大值是40×4=160<888.
当4<t≤9时,-12t2+200t+208=888,即3t2-50t+85=0,
解得:t1=$\frac{25+\sqrt{370}}{3}$(舍去),t2=$\frac{25-\sqrt{370}}{3}$.
则t=$\frac{25-\sqrt{370}}{3}$.
当9<t≤$\frac{65}{4}$时,200t-180=888,
解得:t=$\frac{267}{50}$<9(舍去).
总之,当t=$\frac{25-\sqrt{370}}{3}$时,S恰好是888.
点评 本题考查了正方形的性质和相似三角形的判定与性质以及勾股定理的应用,正确进行讨论是解决本题的关键.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面上有A、B、C三点.
如图,平面上有A、B、C三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}x}$ | B. | $\sqrt{18x}$ | C. | $\sqrt{3x}$ | D. | $\sqrt{{x}^{2}y}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com