
【题目】如图,已知二次函数y= ![]() x2﹣
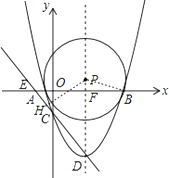
x2﹣ ![]() x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
【答案】(4,0)或(4, ![]() )
)
【解析】解:当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣3=0,解得x1=﹣1,x2=9,则A(﹣1,0),B(9,0),
x﹣3=0,解得x1=﹣1,x2=9,则A(﹣1,0),B(9,0),
当x=0时,y= ![]() x2﹣
x2﹣ ![]() x﹣3=﹣3,则C(0,﹣3),
x﹣3=﹣3,则C(0,﹣3),
∵y= ![]() x2﹣
x2﹣ ![]() x﹣3=
x﹣3= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]() ,
,
∴抛物线的对称轴为直线x=4,D点坐标为(4,﹣ ![]() ),
),
设直线CD的解析式为y=kx+b,
把C(0,﹣3),D(4,﹣ ![]() )代入得
)代入得 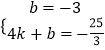 ,解得
,解得 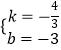 ,
,
∴直线CD的解析式为y=﹣ ![]() x﹣3,
x﹣3,
过P点作PH⊥直线CD于H,连结PB,CD交x轴于E点,抛物线的对称轴交x轴于F点,如图,则F(4,0),E(﹣ ![]() ,0),
,0),
∴EF=4﹣(﹣ ![]() )=
)= ![]() ,FB=
,FB= ![]() ,
,
∴DE= ![]() =
= ![]() ,
,
设P(4,t),则PD=t+ ![]() ,PB=
,PB= ![]() =
= ![]() ,
,
∵以P为圆心的圆经过A,B两点,并且和直线CD相切,
∴PH=PB= ![]() ,
,
∵∠PDH=∠EDF,
∴Rt△DPH∽Rt△DEF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得8t2﹣75t=0,解得t1=0,t2= ![]() ,
,
∴P点坐标为(4,0)或(4, ![]() ).
).
所以答案是(4,0)或(4, ![]() ).
).
【考点精析】掌握二次函数的性质和切线的性质定理是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
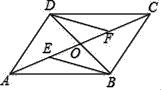
【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如下图.

请你根据统计图中的信息,解答下列问题:
(1)补全条形图和扇形图;
(2)该校学生最喜欢借阅哪类图书?
(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合并下列多项式中的同类项:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣![]() a2b
a2b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com