Question

5．车辆转弯时，能否顺利通过直角弯道的标准是：车辆是否可以行使到和路的边界夹角是45°的位置（如图1中②的位置），例如，图2是某巷子的俯视图，巷子路面宽4cm，转弯处为直角，车辆的车身为矩形ABCD，CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，则车辆就能通过．
（1）试说明长8cm，宽3cm的消防车不能通过该直角转弯；
（2）为了能使长8m，宽3m的消防车通过该弯道，可以将转弯处改为圆弧（分别是以O为圆心，以OM和ON为半径的弧），具体方案如图3，其中OM⊥OM′，请你求出ON的最小值．

Answer 1

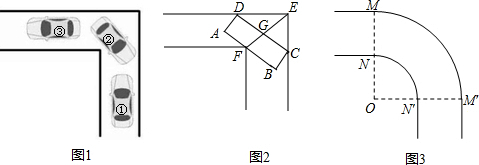
分析 （1）过点F作FH⊥EC于点H，根据道路的宽度求出FH=EH=4m，然后根据等腰直角三角形的性质求出EF、GE的长度，相减即可得到GF的长度，如果不小于车身宽度，则消防车能通过，否则，不能通过；
（2）假设车身C、D分别与点M′、M重合，根据等腰直角三角形的性质求出OG=$\frac{1}{2}$CD=4，OC=$\sqrt{2}$CG=4$\sqrt{2}$，然后求出OF的长度，从而求出可以通过的车宽FG的长度，如果不小于车宽，则消防车能够通过，否则，不能通过；设ON=x，表示出OC=x+4，OG=x+3，又OG=$\frac{1}{2}$CD=4，在Rt△OCG中，利用勾股定理列式进行计算即可求出ON的最小值．

解答 解：（1）消防车不能通过该直角转弯．
理由如下：如图，作FH⊥EC，垂足为H，
∵FH=EH=4，
∴EF=4$\sqrt{2}$，且∠GEC=45°，
∵GC=4，
∴GE=GC=4，
∴GF=4$\sqrt{2}$-4＜3，
即GF的长度未达到车身宽度，
∴消防车不能通过该直角转弯；

（2）若C、D分别与M′、M重合，则△OGM为等腰直角三角形，
∴OG=4，OM=4$\sqrt{2}$，
∴OF=ON=OM-MN=4$\sqrt{2}$-4，
∴FG=OG-OF=$\frac{1}{2}$×8-（4$\sqrt{2}$-4）=8-4$\sqrt{2}$＜3，
∴C、D在$\widehat{MM′}$上，
设ON=x，连接OC，在Rt△OCG中，
OG=x+3，OC=x+4，CG=4，
由勾股定理得，OG²+CG²=OC²，
即（x+3）²+4²=（x+4）²，
解得x=4.5．
答：ON至少为4.5米．

点评 本题考查了等腰直角三角形的性质，勾股定理的应用，读懂题目信息，把实际问题转化为数学问题并构造出等腰直角三角形是解题的关键．