
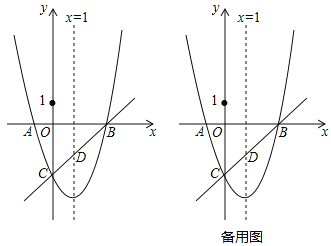
【题目】已知抛物线![]() 与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求出抛物线的函数表达式;
(2)设点E时抛物线上一点,且S△ABE=![]() S△ABC,求tan∠ECO的值;
S△ABC,求tan∠ECO的值;
(3)点P在抛物线上,点Q在抛物线对称轴上,若以B、C、P、Q为顶点的四边形是平行四边形,求点P坐标。
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)(4,5);(-2,5)(2,-3);
;(3)(4,5);(-2,5)(2,-3);
【解析】
(1)利用抛物线的对称轴方程可计算出b=-2,再把C(0,-3)代入抛物线解析式可得到c=-3,所以抛物线的函数表达式为y=x2-2x-3;
(2)先求得S△ABC=6,然后求得S△ABE=![]() S△ABC=10,进而求得E的纵坐标,代入抛物线的解析式求得E的坐标,过点E作EF⊥y轴于点F,然后在Rt△EOF中,利用正切的定义求解即可;
S△ABC=10,进而求得E的纵坐标,代入抛物线的解析式求得E的坐标,过点E作EF⊥y轴于点F,然后在Rt△EOF中,利用正切的定义求解即可;
(3)此题应分两种情况讨论:
①BC为平行四边形的边;那么将点Q向左或向右平移BC长,即可得到点P的横坐标,再代入抛物线的解析式中求解即可;
②BC为平行四边形的对角线;则P的横坐标为2,再代入抛物线的解析式中求解即可.
解:(1)∵抛物线交y轴于点C,
∴c=-3
又∵对称轴是x=1,
∴![]() =1,解得b=-2,
=1,解得b=-2,
∴抛物线表达式为:y=x2-2x-3;
(2)∵抛物线与x轴交于A、B两点
∴A(-1,0)B(3,0),C(0,-3),
∴AB=4,OC=3,
∴S△ABC=![]() ABOC=6,
ABOC=6,
设点E(x,y)
∵S△ABE=![]() S△ABC,
S△ABC,
∴S△ABE=10,
∴S△ABE=![]() AB|yE|=10,
AB|yE|=10,
即:|y|=5,
∵点E在抛物线上
∴x2-2x-3=5或x2-2x-3=-5,
解得:x=4或x=-2,
∴点E(4,5)或E(-2,5),
过点E作EF⊥y轴于点F,如图1,
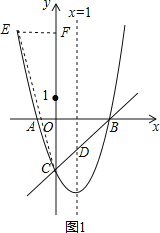
∴EF=4或2,CF=8,
在Rt△EOF中,tan∠ECO=![]() ,
,
∴tan∠ECO=![]() 或tan∠ECO=
或tan∠ECO=![]() .
.
(3)由抛物线的对称轴为x=1,设Q(1,yQ),如图2,
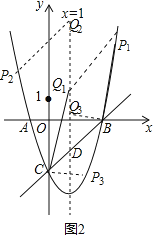
则有:
①若BC为边,
∵B(3,0),C的横坐标与Q的横坐标的差为1,
∴P与B的横坐标的差为1,
∵
∴P的横坐标为4或-2,
则:P(4,yP)或(-2,yP),
把x=4代入抛物线的解析式中,得:y=42-2×4-3=5,
把x=-2代入抛物线的解析式中,得:y=(-202-2×(-2)-3=5,
∴P1(4,5),P2(-2,5);
②若BC为对角线,则P(2,yP),代入抛物线的解析式中,可得:P(2,-3).
综上,存在符合条件的点P,坐标为(4,5)或(-2,5)或(2,-3).


科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形中,点E在BC边上,连接AE.O为AE中点,连接BO并延长交AD于F.
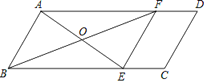
(1)求证:△AOF≌△BOE,
(2)判断当AE平分∠BAD时,四边形ABEF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]()

(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当![]() 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?
(3)![]() 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中![]() 过点
过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作直线
作直线![]() 轴交
轴交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当四边形
.当四边形![]() 的面积为6时,请判断线段
的面积为6时,请判断线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若由乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙两队先合做10天,那么余下的工程由乙队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
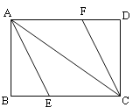
【题目】如图,在矩形ABCD中,AE平分∠BAC交BC于E,CF平分∠ACD交AD于F.
(1)试说明四边形AECF为平行四边形;
(2)探索:当矩形ABCD的边AB和BC满足什么数量关系时,四边形AECF为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年2月28日,前央视知名记者柴静推出了关于雾霾的纪录片——《穹顶之下》,引起了极大的反响.某市准备加大对雾霾的治理力度,2015年第一季度投入资金![]() 万元,第二季度和第三季度计划共投入资金
万元,第二季度和第三季度计划共投入资金![]() 万元,求这两个季度计划投入资金的平均增长率.设这两个季度计划投入资金的平均增长率为
万元,求这两个季度计划投入资金的平均增长率.设这两个季度计划投入资金的平均增长率为![]() ,根据题意可列方程为__________.
,根据题意可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
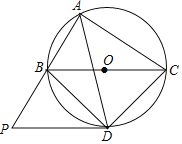
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=3,AC=4,求线段PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com