
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
(1)如图①,![]() 中,
中,![]() ,若
,若![]() ,点
,点![]() 是斜边
是斜边![]() 上一动点,求线段
上一动点,求线段![]() 的最小值.
的最小值.

在组内经过合作交流,得到了如下的解决方法:
根据直线外一点和直线上各点连接的所有线段中,垂线段最短,得到:
当![]() 时,线段
时,线段![]() 取得最小值.请你根据小明的思路求出这个最小值.
取得最小值.请你根据小明的思路求出这个最小值.
(思维运用)
(2)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一动点,过
上一动点,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求线段
,求线段![]() 的最小值.
的最小值.

(问题拓展)
(3)如图,![]() ,
,![]() 线段
线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() 在一条直线上.
在一条直线上.![]() ,
,![]() 分别是对角线
分别是对角线![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 之间的距离的最小值为_____.(直接写出结果,不需要写过程)
之间的距离的最小值为_____.(直接写出结果,不需要写过程)

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用三角形的面积相等即可求解;
(2)连接CM,先证明四边形CDME是矩形,得出DE=CM,再由三角形的面积关系求出CM的最小值,即可得出结果.
(3)连接PM、PN.首先证明∠MPN=90°,设PA=2a,则PB=6-2a,PM=a,PN=![]() (3-a),构建二次函数,利用二次函数的性质即可解决问题;
(3-a),构建二次函数,利用二次函数的性质即可解决问题;
解:(1)如图,当![]() 时,线段
时,线段![]() 取得最小值.
取得最小值.
∵![]() 中,
中,![]() ,
,![]() ,
,
∴AB=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
故CM的最小值为![]() .
.
(2)连接CM,如图所示:
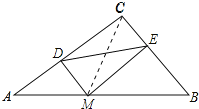
∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠C=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB=![]()
当CM⊥AB时,CM最短,
∵![]()
∴![]() ,
,
∴![]()
∴线段DE的最小值为![]() ;
;
故答案为:![]() .
.
(3)连接PM、PN.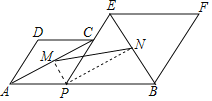
∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,
∴∠APC=120°,∠EPB=60°,
∵M,N分别是对角线AC,BE的中点,
∴∠CPM=![]() ∠APC=60°,∠EPN=
∠APC=60°,∠EPN=![]() ∠EPB=30°,
∠EPB=30°,
∴∠MPN=60°+30°=90°,
设PA=2a,则PB=6-2a,PM=a,PN=![]() (3-a),
(3-a),
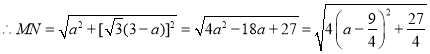 ,
,
∴a=![]() 时,点M,N之间的距离最短,最短距离为
时,点M,N之间的距离最短,最短距离为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
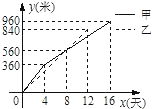
【题目】某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图像,请根据图像所提供的信息,求该公路的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强![]() (kPa)是气体体积
(kPa)是气体体积![]() (m3)的反比例函数,其图像如图所示.
(m3)的反比例函数,其图像如图所示.

(1)求这个反比例函数的表达式;
(2)当气球内的体积为气体1.6m3时,求气体压强![]() 的值:
的值:
(3)当气球内的气体压强大于150kPa时,气球将爆炸,为了安全起见,气体的体积不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线过A(-1,0)、B(3,0)、C(0,-1)三点.
(1)求该抛物线的表达式;
(2)若该抛物线的顶点为D,求直线AD的解析式;
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点标.P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阴影部分是边长是![]() 的大正方形剪去一个边长是
的大正方形剪去一个边长是![]() 的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3幅图割拼方法中,其中能够验证平方差公式有___________(填序号)
的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3幅图割拼方法中,其中能够验证平方差公式有___________(填序号)
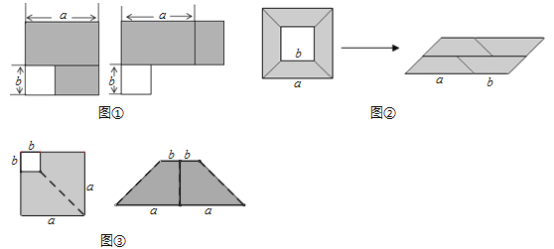
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1.

(1)在方格纸中画△ABC,使AB=![]() ,AC=
,AC=![]() ,BC=4;
,BC=4;
(2)请你用所学的知识验证所画的△ABC是不是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com