
 如图抛物线y=
如图抛物线y= ,x轴于A、B两点,交y轴于点C,顶点为D.
,x轴于A、B两点,交y轴于点C,顶点为D.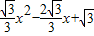 ,
,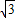
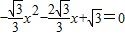 ,
, )(3分)
)(3分) ∵C(0,
∵C(0,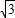 ),
),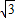 ,
,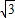 )(5分)
)(5分)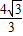 )
)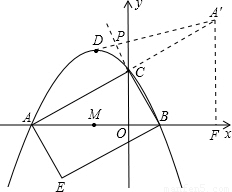 则点P是使△PAD周长最小的点.(10分)
则点P是使△PAD周长最小的点.(10分) ,
, ,
,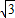 )
)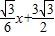
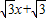
 ,
,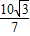 ).(12分)
).(12分)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由.
线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由.查看答案和解析>>
科目:初中数学 来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版) 题型:解答题
 如图抛物线y=
如图抛物线y=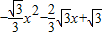 ,x轴于A、B两点,交y轴于点C,顶点为D.
,x轴于A、B两点,交y轴于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源:第26章《二次函数》中考题集(41):26.3 实际问题与二次函数(解析版) 题型:解答题
 如图抛物线y=
如图抛物线y= ,x轴于A、B两点,交y轴于点C,顶点为D.
,x轴于A、B两点,交y轴于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源:2009年浙江省丽水市缙云县新建中学第二次月考数学试卷(解析版) 题型:解答题
 (2006•岳阳)如图抛物线y=
(2006•岳阳)如图抛物线y= ,x轴于A、B两点,交y轴于点C,顶点为D.
,x轴于A、B两点,交y轴于点C,顶点为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com