
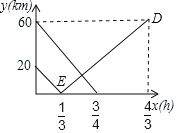
【题目】在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
(1)直接写出连接A、B两市公路的路程以及货车由B市到达A市所需时间.
(2)求机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式.
(3)求机场大巴与货车相遇地到机场C的路程.
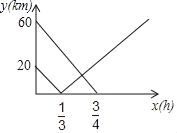
【答案】(1)连接A、B两市公路的路程为80km,货车由B市到达A市所需时间为![]() h;(2)y=﹣80x+60(0≤x≤
h;(2)y=﹣80x+60(0≤x≤![]() );(3)机场大巴与货车相遇地到机场C的路程为
);(3)机场大巴与货车相遇地到机场C的路程为![]() km.
km.
【解析】分析:(1)根据![]() 可求出连接A、B两市公路的路程,再根据货车
可求出连接A、B两市公路的路程,再根据货车![]() h行驶20km可求出货车行驶60km所需时间;
h行驶20km可求出货车行驶60km所需时间;
(2)根据函数图象上点的坐标,利用待定系数法即可求出机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式;
(3)利用待定系数法求出线段ED对应的函数表达式,联立两函数表达式成方程组,通过解方程组可求出机场大巴与货车相遇地到机场C的路程.
详解:(1)60+20=80(km),
![]() (h).
(h).
∴连接A.B两市公路的路程为80km,货车由B市到达A市所需时间为![]() h.
h.
(2)设所求函数表达式为y=kx+b(k≠0),
将点(0,60)、![]() 代入y=kx+b,
代入y=kx+b,
得: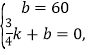 解得:
解得:![]()
∴机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式为![]()
(3)设线段ED对应的函数表达式为y=mx+n(m≠0),
将点![]() 代入y=mx+n,
代入y=mx+n,
得: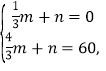 解得:
解得:![]()
∴线段ED对应的函数表达式为![]()
解方程组![]() 得
得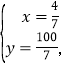
∴机场大巴与货车相遇地到机场C的路程为![]() km.
km.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
⑴画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
⑵画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
⑶在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
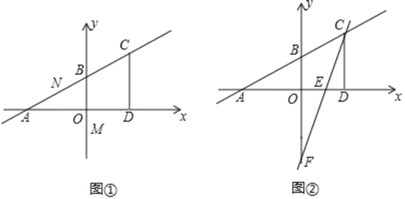
【题目】如图,直线AB:y=![]() x+2与x轴、y轴分别交于A,B两点,C是第一象限内直线AB上一点,过点C作CD⊥x轴于点D,且CD的长为
x+2与x轴、y轴分别交于A,B两点,C是第一象限内直线AB上一点,过点C作CD⊥x轴于点D,且CD的长为![]() ,P是x轴上的动点,N是直线AB上的动点.
,P是x轴上的动点,N是直线AB上的动点.
(1)直接写出A,B两点的坐标;
(2)如图①,若点M的坐标为(0,![]() ),是否存在这样的P点.使以O,P,M,N为顶点的四边形是平行四边形?若有在,请求出P点坐标;若不存在,请说明理由.
),是否存在这样的P点.使以O,P,M,N为顶点的四边形是平行四边形?若有在,请求出P点坐标;若不存在,请说明理由.
(3)如图②,将直线AB绕点C逆时针旋转交y轴于点F,交x轴于点E,若旋转角即∠ACE=45°,求△BFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为__________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把下列各数分别填在相应的集合里:
![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,……
,……
正有理数集合:{ …}
整数集合:{ …}
分数集合:{ …}
(2)在下面的数轴上表示下列各数,并按照从小到大的顺序用“<”号连接起来
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司销售部门提供了某种产品销售收入(记为: ![]() /元)、销售成本(记为:
/元)、销售成本(记为:![]() /元)、销售量(记为:
/元)、销售量(记为: ![]() /吨)方面的信息如下:
/吨)方面的信息如下:
①![]() 时,
时,![]() ;
;
②![]() 时,
时,![]()
![]() ;
;
③![]() 与
与![]() 成正比例函数关系;④
成正比例函数关系;④![]() 与
与![]() 成一次函数关系.
成一次函数关系.
依据上述信息,解决下列问题:
(1)分别求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)销售量为多少吨时,销售收入与销售成本相同?
(3)若销售量为![]() 吨时,求公司的利润. (利润=销售收入-销售成本)
吨时,求公司的利润. (利润=销售收入-销售成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
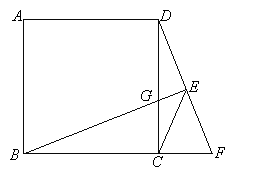
【题目】在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
(1)若正方形ABCD边长为3,DF=4,求CG的长;
(2)求证:EF+EG=![]() CE.
CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com