Question

如图所示，已知DE⊥BC于E，FG⊥BC于G，∠1＝∠2，EH∥AC能成立吗？为什么？

Answer 1

答案：
解析：

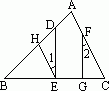
能成立． 　　解法一：连结EF(如图所示)． 　　因为DE⊥BC，FG⊥BC(已知)，所以DE∥FG(在同一平面内垂直于同一条直线的两直线平行)． 　　所以∠3＝∠4(两直线平行，内错角相等)． 　　因为∠1＝∠2(已知)，所以∠1＋∠3＝∠2＋∠4(等量代换)，所以∠HEF＝∠CFE． 　　所以EH∥AC(内错角相等，两直线平行)． 　　解法二：延长HE与FG的延长线交于P(如图所示)． 　　仿解法一DE∥FG，所以∠1＝∠P(两直线平行，同位角相等)． 　　因为∠1＝∠2(已知)，所以∠P＝∠2(等量代换)． 　　所以HE∥AC(内错角相等，两直线平行) 　　解法三：延长ED与CA的延长线交于Q(如图所示)， 　　仿解法一DE∥FG． 　　所以∠2＝∠Q(两直线平行，同位角相等)． 　　因为∠1＝∠2(已知)，所以∠1＝∠Q(等量代换)． 　　所以EH∥CA(内错角相等，两直线平行)．

提示：

提示：本题用了三种解法，一题多解为本题创新之处．