
| A. | (1)和(3) | B. | (2)和(4) | C. | (3)和(4) | D. | 1)和(4) |
分析 根据二次根式的加法法则对各小题进行逐一分析即可.
解答 解:(1)$\sqrt{2}$与$\sqrt{5}$不是同类项,不能合并,故本小题错误;
(2)5$\sqrt{x}$-2$\sqrt{x}$=3$\sqrt{x}$,故本小题正确;
(3)$\frac{\sqrt{8}+\sqrt{50}}{2}$=$\frac{2\sqrt{2}+5\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{2}$≠7,故本小题错误;
(4)3$\sqrt{3a}$+$\sqrt{27a}$=3$\sqrt{3a}$+3$\sqrt{3a}$=6$\sqrt{3a}$,故本小题正确.
故选B.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 随着抛掷次数的增加,正面向上的频率越来越小 | |
| B. | 当抛掷的次数n很大时,正面向上的次数一定为$\frac{n}{2}$ | |
| C. | 不同次数的试验,正面向上的频率可能会不相同 | |
| D. | 连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率小于$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
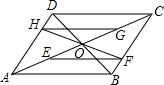 如图,?ABCD的两条对角线AC、BD相交于点O,E、G分别是OA、OC的中点,过点O作任一条直线交AD于点H,交BC于点F,猜想EF与HG的关系,并证明你的猜想.
如图,?ABCD的两条对角线AC、BD相交于点O,E、G分别是OA、OC的中点,过点O作任一条直线交AD于点H,交BC于点F,猜想EF与HG的关系,并证明你的猜想.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com