【答案】
分析:分为以下情况:当最大角是72°时,如图∠A=36°,AD=BD=BC;
②当最大角是90°时,如图∠B=36°,AD=AC,CD=BD;
③当最大角是108°时,如图∠B=36°,BD=AB,AD=DC;
④当最大角是132°时,如图∠ABC=36°,AD=BD,CD=BC,
⑤当最大角是∠A=126°,∠B=36°,AD=AB=CD.
解答:解:当36度的角是所在的小等腰三角形的底角时:
另一个三角形的腰是36°角所在三角形的腰时:∠A=36°,AD=BD=BC,则最大角是72°;

,
另一个三角形的腰是36°角所在三角形的底边时:
有两种情况:
①∠A=36°,AD=BD,CD=BD,当最大角是90°;
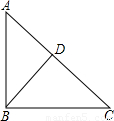
②当最大角是108°时,如图∠B=36°,BD=AB,AD=DC,

当最大角是132°时,如图∠ABC=36°,AD=BD,CD=BC,

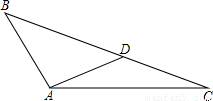
当最大角是∠A=126°,∠B=36°,AD=AB=CD(如图),
故答案为:72°,90°,108°,132°126°.
点评:本题主要考查了等腰三角形的性质及三角形内角和定理;分情况讨论是解决本题的关键,本题有一定的难度,大部分学生思考没那么全面.

 ,
,




