练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
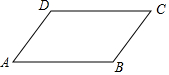
    6．如图，若平行四边形ABCD中，AB=6，AD=4，∠B=150°，则平行四边形ABCD的面积为（　　）
    A．6B．12C．12$\sqrt{3}$D．24

    分析 作平行四边形的高DE，由平行四边形的性质求出∠A=30°，由含30°角的直角三角形的性质求出DE，即可求出平行四边形的面积．

    解答 解：作DE⊥AB于E，如图所示
    ∵四边形ABCD是平行四边形，
    ∴AD=BC=4，AD∥BC，
    ∴∠A+∠B=180°，
    ∴∠A=30°，
    ∴DE=$\frac{1}{2}$AD=2，
    ∴S?ABCD=AB•DE=6×2=12．
    故选：B．

    点评 本题考查了平行四边形的性质、含30°角的直角三角形的性质、平行四边形面积的计算；熟练掌握平行四边形的性质，求出AB边上的高DE是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．如图，在Rt△ABC中，∠B=90°，分别以点A、C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧相交于点M、N，作直线MN，与AC、BC分别交于点D、E，连接AE，当AB=3，AC=5时，△ABE的周长等于（　　）
    A．5B．6C．7D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．计算（-6）+（-2）的结果等于（　　）
    A．8B．-8C．12D．-12

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，每一幅图中均含有若干个菱形，第①幅图中含有1个菱形；第②幅图中含有5个菱形；…按这样的规律下去，则第⑦幅图中含有的菱形的个数为（　　）
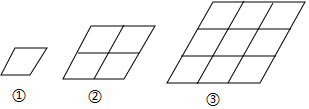
    A．50B．80C．91D．140

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

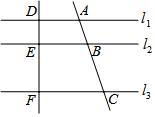    1．如图，直线L1∥L2∥L3，直线AC分别交，L1，L2，L3于点A，B，C，直线DF分别交，L1，L2，L3于点D，E，F．若DE=3，EF=6，AB=4，则AC的长是（　　）
    A．6B．8C．9D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．随着移动互联网的快速发展，OFO、摩拜等互联网共享单车应运而生并快速发展．小冬骑的摩拜单车，爸爸骑的摩托车，沿相同路线由A地到B地，行驶过程中路程y和时间x的函数关系的图象如图，根据图象分析，何时俩人相遇，谁先到（　　）
    A．4分钟时相遇，爸爸先到B．20分钟时相遇，爸爸先到
    C．4分时相遇，小冬先到D．20分钟时相遇，小冬先到

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

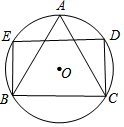    18．如图，⊙O的半径为1，△ABC是⊙O的内接等边三角形，点D、E在圆上，四边形BCDE为矩形，这个矩形的面积是（　　）
    A．2B．$\frac{3}{2}$C．$\sqrt{3}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，某同学家在A处，现在该同学要去位于B处的同学家去玩，请帮助他选择一条最近的路线（　　）
    A．A→C→D→BB．A→C→F→BC．A→C→E→F→BD．A→C→M→B

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）=$\frac{p}{q}$．
    例如12可以分解成1×12，2×6或3×4，因为12-1＞6-2＞4-3，所以3×4是12的最佳分解，所以F（12）=$\frac{3}{4}$．
    （1）如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．
    求证：对任意一个完全平方数m，总有F（m）=1；
    （2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；
    （3）在（2）所得“吉祥数”中，求F（t）的最大值．

    查看答案和解析>>

    同步练习册答案