
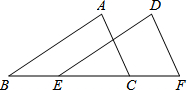
 如图,已知点B,E,C,F在同一条直线上,且BE=CF,AB∥DE,AB=DE.求证:△ABC≌△DEF.
如图,已知点B,E,C,F在同一条直线上,且BE=CF,AB∥DE,AB=DE.求证:△ABC≌△DEF.  开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英得1分,否则小丽得1分,这个游戏对双方公平吗?说明理由?(红色+蓝色=紫色,配成紫色者胜)
小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英得1分,否则小丽得1分,这个游戏对双方公平吗?说明理由?(红色+蓝色=紫色,配成紫色者胜)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知a是最大的负整数,且b、c满足|b-1|+(c+6)2=0.
已知a是最大的负整数,且b、c满足|b-1|+(c+6)2=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com