Question

四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质．只要善于观察、乐于探索我们还会发现更多的结论．

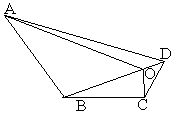
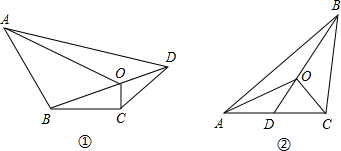
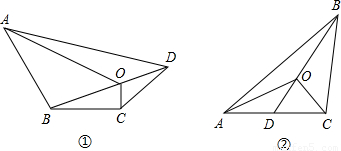
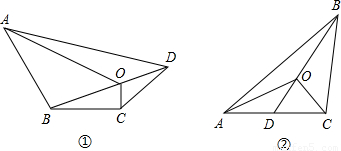
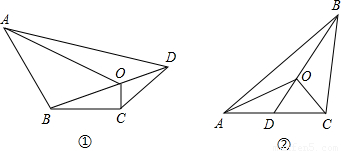
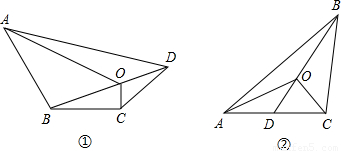
(1)四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形(如图①)，其中相对的两对三角形的面积之积相等．你能证明这个结论吗？试试看．

已知：在四边形ABCD中O是对角线BD主任意一点(如图①)．

求证：S_△OBC·S_△OAD＝S_△OAB·S_△OCD；

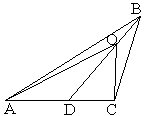
(2)在三角形中(如图②)，你能否归纳出类似的结论？若能，写出你猜想的结论，并证明；若不能，说明理由．

Answer 1

答案：
解析：

(1)分别过点A、C，作AE⊥DB，交DB的延长线于E，CF⊥BD于F，则有S△AOB＝BO·AE，S△COD＝DO·CF，S△AOD＝DO·AE，S△BOC＝BO·CF，∴S△AOB·S△COD＝BO·DO·AE·CF，S△AOD·S△BOC＝BO·DO·CF·AE，∴S△AOB·S△COD＝S△AOD·S△BOC; 　　(2)能．从三角形的一个顶点与对边上任意、点的连线上任取一点，与三角形的另外两个顶点的连线，将三角形分成四个小三角形，其中相对的两对三角形的面积之积相等，或S△COD·S△BOC＝S△AOB·S△DOC．已知：在△ABC中，D为AC上一点，O为BD上一点．求证：S△AOD·S△BOC＝S△AOB·S△DOC．证明：分别过点A、C，作AE上BD，交BD的延长线于E，作CF⊥BD于F，则有：S△AOD＝DO·AE，S△BOC＝BO·CF，S△OAB＝BO·AE，S△DOC＝OD·CF，S△AOD·S△BOC＝BO·DO·CF·AE，∴S△OAB·S△DOC＝BO·DO·AE·CF，∴S△AOD·S△BOC＝S△OAB·S△DOC