
| A. | [(+6$\frac{1}{3}$)+(+4$\frac{2}{3}$)+18]+[(-18)+(-6.8)+(-3.2)] | B. | [(+6$\frac{1}{3}$)+(-6.8)+(+4$\frac{2}{3}$)]+[(-18)+18+(-3.2)] | ||
| C. | [(+6$\frac{1}{3}$)+(-18)]+[(+4$\frac{2}{3}$)+(-6.8)]+[18+(-3.2)] | D. | [(+6$\frac{1}{3}$)+(+4$\frac{2}{3}$)]+[(-18)+18]+[(-3.2)+(-6.8)] |
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
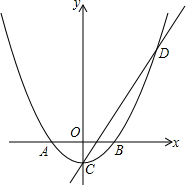 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,长方体的长、宽、高分别为5cm、3cm、2cm,一只蚂蚁欲从长方体底面上的点A沿着长方体表面爬到点B处,则蚂蚁需要爬行的最短路程的长为5$\sqrt{2}$cm.
如图,长方体的长、宽、高分别为5cm、3cm、2cm,一只蚂蚁欲从长方体底面上的点A沿着长方体表面爬到点B处,则蚂蚁需要爬行的最短路程的长为5$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D.
如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com