
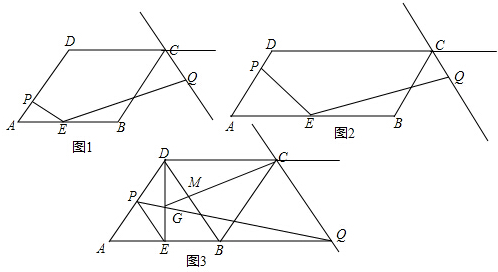
分析 (1)如图1中,作EG⊥AD于G,EN⊥CQ于N,延长CQ、AB交于点M,先证明△EAG∽△EMN得$\frac{AE}{EM}$=$\frac{EG}{EN}$=$\frac{1}{3}$,再证明△EPG∽△ENQ,得$\frac{PE}{EQ}$=$\frac{EG}{EN}$=$\frac{1}{3}$即可证明.
(2)结论:EQ=2EP.如图2中,连接EC,作EG⊥AD于G,证明方法类似(1).
(3)如图3中,当点P是线段AD中点时,点Q在AB的延长线上,由BN∥PE,得到$\frac{BN}{PE}$=$\frac{BC}{CE}$=$\frac{2}{3}$,设PE=a,则DB=2a,BN=$\frac{2}{3}$a,DN=$\frac{4}{3}$a,求出GN与NQ的比值即可解决问题.
解答 (1)证明:如图1中,作EG⊥AD于G,EN⊥CQ于N,延长CQ、AB交于点M.
∵四边形ABCD是平行四边形,DC=BC,∠A=60°,
∴AB=BC=CD=AD,
∴△ABD,△BDC都是等边三角形,
∵CM是∠DCB的外角平分线,
∴∠BCM=∠CBM=60°,
∴△BCM是等边三角形,
∵AE=EB,AB=BC=BM,
∴EM=3AE,
∵∠AGE=∠ENM=90°,∠A=∠M=60°,
∴△EAG∽△EMN,
∴$\frac{AE}{EM}$=$\frac{EG}{EN}$=$\frac{1}{3}$,
∵∠AEG=∠MEN=30°,
∴∠GEN=∠PEQ=120°,
∴∠PEG=∠QEN,
∵∠EGP=∠EQN=90°,
∴△EPG∽△ENQ,
∴$\frac{PE}{EQ}$=$\frac{EG}{EN}$=$\frac{1}{3}$,
∴EN=3PE.
(2)结论:EQ=2EP.
理由:如图2中,连接EC,作EG⊥AD于G,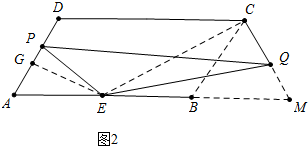
∵AB=CD=2BC,△BCM是等边三角形,AE=EB,
∴BC=BM=EB,
∴∠ECB=90°,
∵∠AGE=∠ECM=90°,∠A=∠M=60°,
∴△EAG∽△EMC,
∴$\frac{AE}{EM}$=$\frac{EG}{EC}$=$\frac{1}{2}$,
∵∠AEG=∠MEC=30°,
∴∠GEC=∠PEQ=120°,
∴∠PEG=∠QEC,
∵∠EGP=∠ECQ=90°,
∴△EPG∽△EQC,
∴$\frac{PE}{EQ}$=$\frac{EG}{EC}$=$\frac{1}{2}$,
∴EQ=2EP.
(3)如图3中,当点P是线段AD中点时,点Q在AB的延长线上,
∵AP=PD,AE=EB,
∴PE∥DB.DE=$\frac{1}{2}$DE,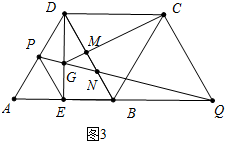
∵BN∥PE,
∴$\frac{BN}{PE}$=$\frac{BC}{CE}$=$\frac{2}{3}$,设PE=a,则DB=2a,BN=$\frac{2}{3}$a,DN=$\frac{4}{3}$a,
∴$\frac{PE}{DN}$=$\frac{PG}{GN}$=$\frac{EG}{DG}$=$\frac{3}{4}$,∵$\frac{PN}{NC}$=$\frac{EB}{BC}$=$\frac{1}{2}$,
∴$\frac{GN}{NC}$=$\frac{GM}{CM}$=$\frac{2}{7}$,
∴MC=$\frac{7}{9}$CG,
∵DE=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$,
∴DG=$\frac{4}{7}$DE=$\frac{8\sqrt{3}}{7}$,
在RT△DCG中,CG=$\sqrt{D{G}^{2}+C{D}^{2}}$=$\sqrt{(\frac{8\sqrt{3}}{7})^{2}+{4}^{2}}$=$\frac{4}{7}$$\sqrt{61}$,
∴CM=$\frac{4\sqrt{61}}{9}$.
点评 本题考查四边形综合题、相似三角形的性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是学会添加常用辅助线构造相似三角形,利用平行线分线段成比例定理是解决第三个问题的关键,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是136°.
如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是136°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 10 | B. | 16 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com