
已知:△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°.
问题1:如图1,若∠ACB=90°,AC= AB,BD=
AB,BD= DC,则
DC,则 的值为_________,
的值为_________, 的值为__________.
的值为__________.

问题2:如图2,若∠ACB为钝角,且AB>AC,BD>DC.

1.(1)求证: ;
;
2.(2)若点E在AD上,且DE=DB,延长CE交AB于点F,求∠BFC的度数.
问题1: ,2
,2
问题2:
1. (1)在AB上截取AG,使AG=AC,连接GD.(如图7)
(1)在AB上截取AG,使AG=AC,连接GD.(如图7)
∵AD平分∠BAC,
∴∠1=∠2.
在△AGD和△ACD中,
 AG
=AC,
AG
=AC,
∠1 =∠2,
AD=AD,
∴△AGD≌△ACD.
∴DG=DC. -------------------------------3分
∵△BGD中,BD-DG<BG,
∴BD-DC<BG.
∵BG= AB-AG= AB-AC,
∴BD-DC<AB-AC
2.(2)∵由(1)知△AGD≌△ACD,
∴GD=CD,∠4 =∠3=60°.
∴∠5 =180°-∠3-∠4=180°-60°-60°=60°.
∴∠5 =∠3.
在△BGD和△ECD中,
 DB
=DE,
DB
=DE,
∠5 =∠3,
DG=DC,
∴△BGD≌△ECD. ----------------5分
∴∠B =∠6.
∵△BFC中,∠BFC=180°-∠B-∠7 =180°-∠6-∠7 =∠3,
∴∠BFC=60°
【解析】略


科目:初中数学 来源: 题型:
| 3 |
| 4 |
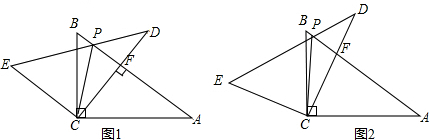
| 25 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.查看答案和解析>>
科目:初中数学 来源: 题型:
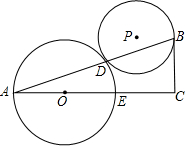 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com