
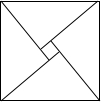
 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )| A. | 25 | B. | 9 | C. | 13 | D. | 169 |
分析 根据大正方形的面积即可求得c2,利用勾股定理可以得到a2+b2=c2,然后求得直角三角形的面积即可求得ab的值,根据(a+b)2=a2+b2+2ab=c2+2ab即可求解.
解答  解:如图,∵大正方形的面积是13,
解:如图,∵大正方形的面积是13,
∴c2=13,
∴a2+b2=c2=13,
∵直角三角形的面积是(13-1)÷4=3,
又∵直角三角形的面积是$\frac{1}{2}$ab=3,
∴ab=6,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2×6=13+12=25.
故选:A.
点评 本题考查了勾股定理以及完全平方公式.注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:
如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=2 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (-$\sqrt{3}$)2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
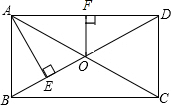 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.| A. | 6 | B. | 9 | C. | 12 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 0.450 | |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | ||
| 1600~1799 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C 在同一水平地面上.
如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C 在同一水平地面上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,5cm,8cm | B. | 1cm,2cm,3cm | C. | 4cm,5cm,10cm | D. | 3cm,4cm,5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
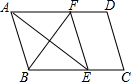 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com