【题目】正方形
、
、
、…按如图所示的方式放置.点
、
、
、…和点
、
、
、…分别在直线
和
轴上，则点
的坐标是__________．（
为正整数）
【答案】
【解析】由图和条件可知A1（0，1）A2（1，2）A3（3，4），B1（1，1），B2（3，2），Bn的横坐标为An+1的横坐标，纵坐标为An的纵坐标，又An的横坐标数列为An=2n-1-1，所以纵坐标为（2n-1），然后就可以求出Bn的坐标为[A（n+1）的横坐标，An的纵坐标]．
由图和条件可知A1（0，1）A2（1，2）A3（3，4），B1（1，1），B2（3，2），
∴Bn的横坐标为An+1的横坐标，纵坐标为An的纵坐标，
又An的横坐标数列为An=2n-1-1，所以纵坐标为2n-1，
∴Bn的坐标为[A（n+1）的横坐标，An的纵坐标]=（2n-1，2n-1）．
故答案为：（2n-1，2n-1）．
小学同步三练核心密卷系列答案科目：初中数学 来源： 题型：
【题目】银泰百货名创优品店购进600个钥匙扣，进价为每个8元，第一周以每个12元的价格售出200个，第二周若按每个12元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售．据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价，单价降低
元销售，销售一周后，商店对剩余钥匙扣清仓处理，以每个6元的价格全部售出．
（1）如果这批钥匙扣共获利1050元，那么第二周每个钥匙扣的销售价格为多少元？
（2）这次降价活动，1050元是最高利润吗？若是，说明理由；若不是，求出最高利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践
问题背景：
我们知道，三角形的中位线平行于三角形的第三边，并且等于第三边的一半，如何证明三角形中位线定理呢?
已知：如图1，在
中，
分别是
的中点．
求证：
问题中既要证明两条线段所在的直线平行，又要证明其中一条线段的长等于另一线段长的一半．所以可以用“倍长法”将
延长一倍：延长到
，使得
，连接
这样只需证明
，且
．由于
是
的中点，容易证明四边形
、四边形
是平行四边形，证明．．．
问题解决：
上述材料中“倍长法”体现的数学思想主要是_____． (填入选项前的字母代号即可)
A．数形结合思想 B．转化思想 C．分类讨论思想 D．方程思想
证明四边形是平行四边形的依据是
反思交流：
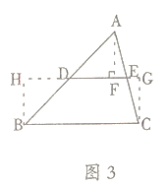
“智慧小组”在证明中位线定理时，在图1的基础上追加了如上辅助线作法：如图3，分别过点
作的垂线，垂足分别为
，．．
请你根据“智慧小组”添加的辅助线，证明三角形的中位线定理．
方法迁移：
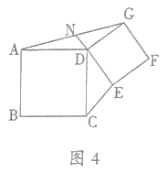
如图4、四边形
和
都是正方形，
是
的中点．求证： 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
（1）请在图中确定该圆弧所在圆心D点的位置，D点坐标为 ；
（2）连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；
（3）若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，CD⊥AB于点D，DA=DC=4，DB=2，AF⊥BC于点F，交DC于点E．
（1）求线段AE的长；
（2）若点G是AC的中点，点M是线段CD上一动点，连结GM，过点G作GN⊥GM交直线AB于点N，记△CGM的面积为S1，△AGN的面积为S2．在点M的运动过程中，试探究：S1与S2的数量关系
查看答案和解析>>
科目：初中数学 来源： 题型：
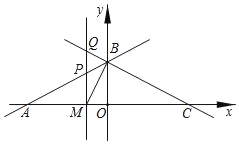
【题目】如图，直线y＝
x+3与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称．
（1）求直线BC的函数表达式；
（2）设点M是x轴上的一个动点，过点M作y轴的平行线，交直线AB于点P，交直线BC于点Q，连接BM．
①若∠MBC＝90°，求点P的坐标；
②若△PQB的面积为
，请直接写出点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，点D在直线BC上，E在AC上，且AC＝CD，DE＝AB．
（1）如图②，将△ECD沿CB方向平移，使点E落在AB上，得△E1C1D1，求平移的距离；
（2）如图③，将△ECD绕点C逆时针旋转，使点E落在AB上，得△E2CD2，求旋转角∠DCD2的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，菱形OABC的OC边落在x轴上，∠AOC=60°，OA=60
．若菱形OABC内部（边界及顶点除外）的一格点P（x，y）满足：x2﹣y2=90x﹣90y，就称格点P为“好点”，则菱形OABC内部“好点”的个数为（ ）
（注：所谓“格点”，是指在平面直角坐标系中横、纵坐标均为整数的点．）
A. 145 B. 146 C. 147 D. 148
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
