
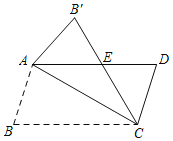
【题目】如图,ABCD中,AB=6,∠B=75°,将△ABC沿AC边折叠得到△AB′C,B′C交AD于E,∠B′AE=45°,则点A到BC的距离为( )
A.2![]() B.3
B.3![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过B′作B′H⊥AD于H,根据等腰直角三角形的性质得到AH=B′H=![]() AB′,根据折叠的性质得到AB′=AB=6,∠AB′E=∠B=75°,求得∠AEB′=60°,解直角三角形得到HE=
AB′,根据折叠的性质得到AB′=AB=6,∠AB′E=∠B=75°,求得∠AEB′=60°,解直角三角形得到HE=![]() B′H,B′E=2
B′H,B′E=2![]() ,根据平行线的性质得到∠DAC=∠ACB,推出AE=CE,根据全等三角形的性质得到DE=B′E=2
,根据平行线的性质得到∠DAC=∠ACB,推出AE=CE,根据全等三角形的性质得到DE=B′E=2![]() ,求得AD=AE+DE=3
,求得AD=AE+DE=3![]() +3
+3![]() ,过A作AG⊥BC于G,根据直角三角形的性质即可得到结论.
,过A作AG⊥BC于G,根据直角三角形的性质即可得到结论.
过B′作B′H⊥AD于H,
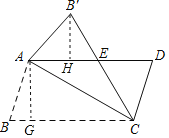
∵∠B′AE=45°,
∴△AB′H是等腰直角三角形,
∴AH=B′H=![]() AB′,
AB′,
∵将△ABC沿AC边折叠得到△AB′C,
∴AB′=AB=6,∠AB′E=∠B=75°,
∴∠AEB′=60°,
∴AH=B′H=![]() ×6=3
×6=3![]() ,
,
∴HE=![]() B′H=
B′H=![]() ,B′E=2
,B′E=2![]() ,
,
∵ABCD中,AD∥BC,
∴∠DAC=∠ACB,
∵∠ACB=∠ACB′,
∴∠EAC=∠ACE,
∴AE=CE,
∵∠AB′E=∠B=∠D,∠AEB′=∠CED,
∴△AB′E≌△CDE(AAS),
∴DE=B′E=2![]() ,
,
∴AD=AE+DE=3![]() +3
+3![]() ,
,
∵∠AEB′=∠EAC+∠ACE=60°,
∴∠ACE=∠CAE=30°,
∴∠BAC=75°,
∴AC=AD
过A作AG⊥BC于G,
∴AG=![]() AC=
AC=![]() ,
,
故选:C.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=53°,且DE=2.4米,求匾额悬挂的高度AB的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
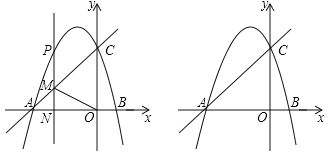
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数t=![]() (其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.
(其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.
(1)根据以上方法求出T(268)= ,T(513)= ;
(2)已知三位数![]() (其中a>b>1)的差数T(
(其中a>b>1)的差数T(![]() )=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.
)=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
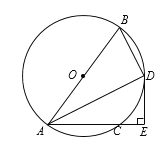
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com