
����Ŀ����ƽ��ֱ������ϵ�У����Dz����Ѻ���������������ȵĵ��Ϊ��֮�㣬���磬�㣨1��1�������� 2���� 2������![]() ��
��![]() ��������������֮�㣬��Ȼ��֮������������
��������������֮�㣬��Ȼ��֮������������
��1������ P��2��b���Ƿ���������![]() (n Ϊ������n �� 0) ��ͼ���ϵ���֮�㣬�������������������ʽ��
(n Ϊ������n �� 0) ��ͼ���ϵ���֮�㣬�������������������ʽ��
��2����O �İ뾶��![]() ��
��
�������O�ϵ�������֮������ꣻ
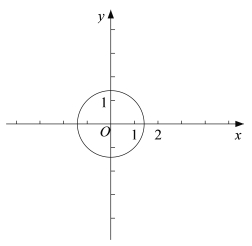
����֪�� M��m��3������ Q �ǣ�1���з���������![]() ͼ�������ڵ� P ����֮�㣬����Q ��ֱ�� l �� y �ύ�ڵ� A����OAQ��45�������ڡ� O �ϴ���һ�� N��ʹ��ֱ�� MN �� l�� MN �� l����� m ��ȡֵ��Χ��
ͼ�������ڵ� P ����֮�㣬����Q ��ֱ�� l �� y �ύ�ڵ� A����OAQ��45�������ڡ� O �ϴ���һ�� N��ʹ��ֱ�� MN �� l�� MN �� l����� m ��ȡֵ��Χ��
���𰸡���1��![]() ����2������O��������֮�������ǣ�1��1����-1��-1������m��ȡֵ��ΧΪ-5��m��-1��1��m��5��
����2������O��������֮�������ǣ�1��1����-1��-1������m��ȡֵ��ΧΪ-5��m��-1��1��m��5��
��������
��1������֮��Ķ�������P�����꣬�����ô���ϵ��������÷�������������ʽ����2�������O�ϵ���֮������Ϊ��a��a������Բ�İ뾶�����ݹ��ɶ����ɵõ�����a�ķ��̣������a��ֵ����ɵ���֮������ꣻ�ڷ���������������ۣ���MNΪy=-x+bʱ��m=b-3����ֱ��MNƽ�������O����ʱ�����е��ڵ�������ʱ��bȡ����Сֵ����ֱ��MNƽ�������O����ʱ�����е��ڵ�һ����ʱ��bȡ�����ֵ���ݴ˿ɵ�m��ȡֵ��ΧΪ-5��m��-1����ֱ��MNΪy=x+bʱ��ͬ���ɵã�m��ȡֵ��ΧΪ1��m��5��
��1�� ��P��2��b������֮������b=2
��P��2��2��
��P��2��2�� ����![]() �е�n=4
�е�n=4
�෴������������ʽ��![]()
��2��������O����֮�������ǣ�![]() ��
��![]() ����
����![]() ��
��![]()
![]() =1��
=1��![]() =-1
=-1
����O��������֮�������ǣ�1��1����-1��-1��
������1��֪�����ڵ�P����֮��Q������Ϊ��-2��-2��
����֪MN��l��MN��l

��ֱ��MNΪy=-x+b��y=x+b
��MNΪy=-x+bʱ��m=b-3
��ͼ��֪����ֱ��MNƽ��������O����ʱ��
���е��ڵ�������ʱ��bȡ����Сֵ��
��ʱMN ��Ϊ![]() ��
��
���� ![]() Ϊ�е㣬
Ϊ�е㣬![]() Ϊֱ����y��Ľ���
Ϊֱ����y��Ľ���
�ߡ�O![]()
![]() Ϊ��Ҫֱ�������Σ�
Ϊ��Ҫֱ�������Σ�
��O![]() =
=![]() ��O
��O![]() =2
=2
��b����Сֵ��-2��
��m����Сֵ��-5
��ֱ��MNƽ��������O����ʱ�����е��ڵڶ�����ʱ��
bȡ�����ֵ����ʱMN ��Ϊ![]() ��
��
���� ![]() Ϊ�е㣬
Ϊ�е㣬![]() Ϊֱ��
Ϊֱ��![]() ��y��Ľ��㡣
��y��Ľ��㡣
ͬ���ɵã�b�����ֵΪ2��m�����ֵΪ-1��
��m��ȡֵ��ΧΪ-5��m��-1��
��ֱ��MNΪy=x+bʱ��
ͬ���ɵã�m��ȡֵ��ΧΪ1��m��5��
����������m��ȡֵ��ΧΪ-5��m��-1��1��m��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˼ӹ�ͬһ���������ÿ��ӹ�����������ÿ��ӹ������� 1.5 �������˸��ӹ� 600 ������������ױ������� 5 �죮
��1����ס�������ÿ����ӹ����ٸ����������
��2����֪�ס������˼ӹ��������ÿ��ļӹ��ѷֱ��� 150 Ԫ�� 120 Ԫ������ 3000 ����������ļӹ��������ӹ�һ��ʱ������а��ţ�ʣ���������ҵ�����ɣ�����ܼӹ��Ѳ����� 7800 Ԫ����ô�����ټӹ��˶����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У���E�DZ�AD�϶��㣬��F�DZ�BC�϶��㣬����EF���Ѿ���ABCD��ֱ��EF�۵�����Bǡ�����ڱ�AD�ϣ���Ϊ��G����ͼ2���Ѿ���չ����ƽ������BE��FG.

��1���ж��ı���BEGF����״һ������ ������֤����Ľ��ۣ�
��2�������α�AB��4��BC��8��ֱ��д���ı���BEGF��������ֵΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
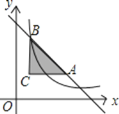
����Ŀ����ͼ������C��1��2���ֱ���x�ᡢy���ƽ���ߣ���ֱ��y=��x+6��A��B���㣬������������![]() ��x��0����ͼ�����ABC�й����㣬��k��ȡֵ��Χ��________��
��x��0����ͼ�����ABC�й����㣬��k��ȡֵ��Χ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����C����O��һ�㣬����C��ֱ�߽�AB���ӳ����ڵ�D��AE��DC������ΪE��F��AE����O�Ľ��㣬ACƽ����BAE��

��1����֤��DE����O�����ߣ�
��2����AE=6����D=30������ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ1���ڡ�ABC�͡�ADE�У�AB=AC=AD=AE������BAC+��DAE=180�� ʱ�����dzơ�ABC���DAE��Ϊ���������������Ρ�����ABC�ı�BC�ϵĸ���AM������ADE�ġ����ľࡱ����A�������������ġ�.
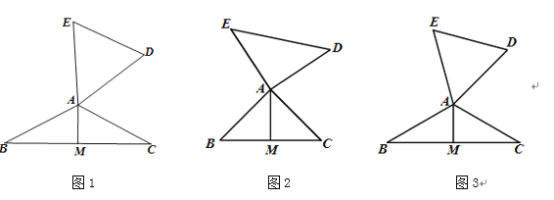
��1��������֪����ͼ2��ͼ3�У���ABC���DAE��Ϊ���������������Ρ���AM�ǡ����ľࡱ��
����ͼ2������BAC=90��ʱ��AM��DE֮���������ϵΪAM=�� ��DE��
����ͼ3������BAC=120�㣬ED=6ʱ��AM�ij�Ϊ�� ����
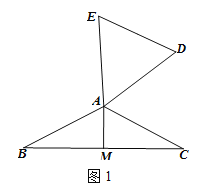
��2��������֤��
��ͼ1�У�����BACΪ�����ʱ������AM��DE֮���������ϵ��������֤����
��3����չӦ��
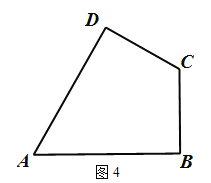
��ͼ4�����ı���ABCD�У�AD=AB��CD=BC����B=90�㣬��A=60�㣬CA=![]() �����ı�ABCD���ڲ��ҵ���P��ʹ�á�PAD���PBC��Ϊ���������������Ρ������ش�����������
�����ı�ABCD���ڲ��ҵ���P��ʹ�á�PAD���PBC��Ϊ���������������Ρ������ش�����������
������ͼ�б����P��λ�ã����������õ��λ��Ϊ ��
��ֱ��д����PBC�ġ����ľࡱ�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı���![]() ��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��![]() ��
��![]() ��AC=4����ƽ���ı���
��AC=4����ƽ���ı���![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת��ʹ��
��ʱ�뷽����ת��ʹ��![]() ����
����![]() ���ϣ�����ת���
���ϣ�����ת���![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ������Ϊ________��
������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxOy�У���A������Ϊ��4��0�����Ե�AΪԲ�ģ�4Ϊ�뾶��Բ��x�ύ��O��B���㣬OCΪ�ң���AOC=60�㣬P��x���ϵ�һ���㣬����CP��
��1��ֱ��д��OC=___________��
��2����ͼ1����CP���A����ʱ����PO�ij���
��3����ͼ2������P��ֱ��OB��ʱ��CP���ӳ������A�ཻ�ڵ�Q���ʵ�POΪ��ֵʱ����OCQ�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���һ�κ���![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() .
.
��1�������![]() ����ƽ��
����ƽ��![]() ����λ��õ�ֱ��
����λ��õ�ֱ��![]() ����
����![]() ��ֵ��
��ֵ��
��2����ֱ��![]() ����
����![]() �͵�
�͵�![]() ʱ����
ʱ����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������ƽ�����е�![]() ������
������![]() ȡ��ֵ����
ȡ��ֵ����![]() ������ֱ��
������ֱ��![]() �ϣ���
�ϣ���![]() �������������.
�������������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com