
【题目】用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板:

(1)观察图形,填写下表:
图形 | (1) | (2) | (3) | …… |
黑色瓷砖的块数 | 4 | …… | ||
黑白两种瓷砖的总块数 | 15 | …… |
(2)依上推测,第n个图形中黑色瓷砖的块数为__________________;黑白两种瓷砖的总块数为__________________(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗?若能,求出是第几个图形;若不能,请说明理由.
【答案】(1)7,10,25,35;(2)![]() ;(3)不能,理由见解析
;(3)不能,理由见解析
【解析】
(1)找出数量上的变化规律,填表即可;
(2)找出数量上的变化规律,从而推出一般性的结论;
(3)利用(2)中得到的代数式列出方程可求解.
(1)第一个图形有黑色瓷砖为![]() 块,黑白两种瓷砖的数为
块,黑白两种瓷砖的数为![]() 块;
块;
第二个图形有黑色瓷砖为![]() 块,黑白两种瓷砖的数为
块,黑白两种瓷砖的数为![]() 块;
块;
第三个图形有黑色瓷砖为![]() 块,黑白两种瓷砖的数为
块,黑白两种瓷砖的数为![]() 块;
块;
图形 | (1) | (2) | (3) | …… |
黑色瓷砖的块数 | 4 | 7 | 10 | …… |
黑白两种瓷砖的总块数 | 15 | 25 | 35 | …… |
(2)
第一个图形有黑色瓷砖为![]() 块,黑白两种瓷砖总数为
块,黑白两种瓷砖总数为![]() 块;
块;
第二个图形有黑色瓷砖为![]() 块,黑白两种瓷砖总数为
块,黑白两种瓷砖总数为![]() 块;
块;
第三个图形有黑色瓷砖为![]() 块,黑白两种瓷砖总数为
块,黑白两种瓷砖总数为![]() 块;
块;
…
第![]() 个图形中需要黑色瓷砖为
个图形中需要黑色瓷砖为![]() 块,黑白两种瓷砖总数为
块,黑白两种瓷砖总数为![]() 块.
块.
故答案为![]()
(3)由(2)得:黑色瓷砖为![]() 块,白瓷砖为
块,白瓷砖为![]() 块,
块,
依题意得:![]()
解得:![]()
因为2011不能被4整除,所以白色瓷砖的块数不能比黑色瓷砖的块数多2014块.


科目:初中数学 来源: 题型:
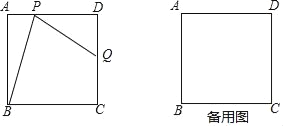
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三个角相等的四边形叫做三等角四边形.
(1)在三等角四边形![]() 中,
中,![]() ,则
,则![]() 的取值范围为________.
的取值范围为________.
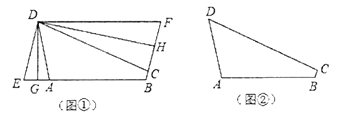
(2)如图①,折叠平行四边形![]() ,使得顶点
,使得顶点![]() 、
、![]() 分别落在边
分别落在边![]() 、
、![]() 上的点
上的点![]() 、
、![]() 处,折痕为
处,折痕为![]() 、
、![]() .求证:四边形
.求证:四边形![]() 为三等角四边形;
为三等角四边形;
(3)如图②,三等角四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长度为多少?
的长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
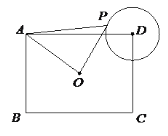
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
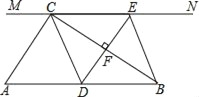
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )个.
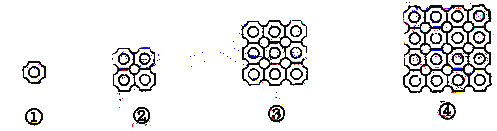
A.145 B.146 C.180 D.181
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:y=y1﹣y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时y=1.
(1)求y关于x的函数关系式.
(2)求x=﹣![]() 时,y的值.
时,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
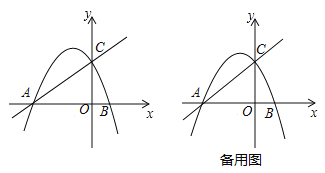
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com