

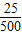 =500,
=500,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《数据收集与处理》(03)(解析版) 题型:解答题
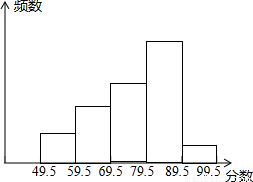
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《因式分解》(03)(解析版) 题型:解答题
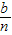 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《代数式》(05)(解析版) 题型:解答题
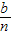 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.查看答案和解析>>
科目:初中数学 来源:2005年江苏省扬州市中考数学试卷(课标卷)(解析版) 题型:解答题
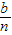 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.查看答案和解析>>
科目:初中数学 来源:2005年江苏省扬州市中考数学试卷(大纲卷)(解析版) 题型:解答题
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com