
,抛物线 交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
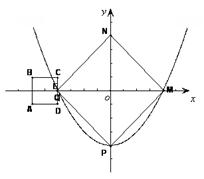
(1)求点M、N的坐标,并判断四边形NMPQ的形状;
(2)如图,坐标系中有一正方形ABCD,其中AB=2cm且CD⊥x轴,CD的中点E与Q点重合,正方形ABCD以1cm/s的速度沿射线QM运动,当正方形ABCD完全进入四边形QPMN时立即停止运动.
①当正方形ABCD与四边形NMPQ的交点个数为2时,求两四边形重叠部分的面积y与运动时间t之间的函数关系式,并写出自变量t的取值范围;
②求运动几秒时,重叠部分的面积为正方形ABCD面积
的一半.
(1)M(4,0) N(0,4),四边形NMPQ是正方形;(2)①y=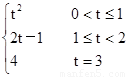
②t=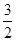
【解析】
试题分析:(1) 抛物线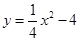 交x轴于点Q、M,交y轴于点P,由图象知M在X轴的正半轴,令y=0,即
交x轴于点Q、M,交y轴于点P,由图象知M在X轴的正半轴,令y=0,即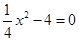 ,解得
,解得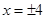 ,所以M的坐标为(4,0),N点的坐标为(-4,0);P点是抛物线与y轴的交点,另x=0,即y=-4,所以P点的坐标(0,-4);点P关于x轴的对称点为N,所以N点的坐标为(0,4);在直角三角形OMP中,由勾股定理得
,所以M的坐标为(4,0),N点的坐标为(-4,0);P点是抛物线与y轴的交点,另x=0,即y=-4,所以P点的坐标(0,-4);点P关于x轴的对称点为N,所以N点的坐标为(0,4);在直角三角形OMP中,由勾股定理得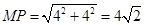 ,同理PQ=
,同理PQ= 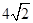 ,MN=
,MN= 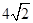 ,QN=
,QN= 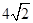 ,所以四边形NMPQ是正方形
,所以四边形NMPQ是正方形
(2)①坐标系中有一正方形ABCD,其中AB=2cm且CD⊥x轴,CD的中点E与Q点重合,CE="DE=1cm;"
当正方形ABCD与四边形NMPQ的交点个数为2时有几种情况,分别为当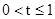 ,正方形ABCD从开始到有一半进入四边形NMPQ,此时两四边形重叠部分的面积y与运动时间t之间的函数关系式为y=
,正方形ABCD从开始到有一半进入四边形NMPQ,此时两四边形重叠部分的面积y与运动时间t之间的函数关系式为y=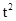 ;当
;当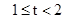 ,正方形ABCD的CD边与四边形NMPQ无交点,而正方形ABCD的AB边开始进入
,正方形ABCD的CD边与四边形NMPQ无交点,而正方形ABCD的AB边开始进入
四边形NMPQ,交点也是2个,此时两四边形重叠部分的面积y与运动时间t之间的函数关系式为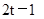 ;当
;当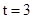 时正方形ABCD的AB边的两端点A、B恰在四边形NMPQ,此时CD与NMPQ无交点,此时两四边形重叠部分的面积为正方形ABCD的面积,即y=4,综上所述
时正方形ABCD的AB边的两端点A、B恰在四边形NMPQ,此时CD与NMPQ无交点,此时两四边形重叠部分的面积为正方形ABCD的面积,即y=4,综上所述
y=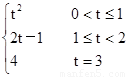
②由(2)知三种情况中只有第二种,重叠部分的面积才可能为正方形ABCD面积的一半,即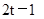 =2,解得t=
=2,解得t=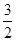
考点:正方形
点评:本题考查正方形,解本题的关键是掌握正方形的概念和性质,本题难度较大


科目:初中数学 来源: 题型:
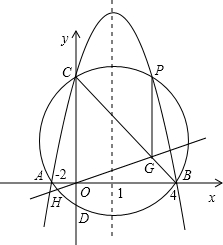 ⊙O′交y轴于另一点D,交抛物线于另一点P,过原点O且垂直于AD的直线交AD于点H,交BC于点G.
⊙O′交y轴于另一点D,交抛物线于另一点P,过原点O且垂直于AD的直线交AD于点H,交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
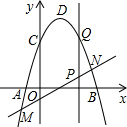 如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:
 AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.
AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
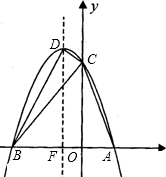 A=45°,tanA=3;
A=45°,tanA=3;查看答案和解析>>
科目:初中数学 来源: 题型:
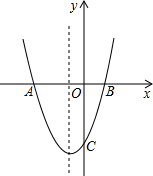 (2013•阜宁县一模)已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴.
(2013•阜宁县一模)已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com