
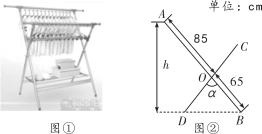
【题目】有一种落地晾衣架如图①所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图②是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85 cm,BO=DO=65 cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为______cm.(参考数据:sin 37°≈0.6,cos 37°≈0.8,sin 53°≈0.8,cos 53°≈0.6)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
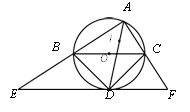
【题目】如图,A是以BC为直径的⊙O上一点,I是△ABC的内心,AI的延长线交⊙O于点D,过点D作BC的平行线交AB、AC的延长线于E、F.下列说法:①△DBC是等腰直角三角形;②EF与⊙O相切;③EF=2BC;④点B、I、C在以点D 为圆心的同一个圆上.其中一定正确的是_______(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量m(件)之间的关系及成本如下表所示:
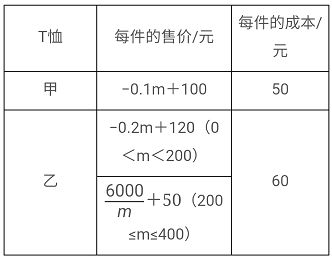
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元.
(2)若所有的T恤都能售完,求该店获得的总利润y(元)与乙种T恤的进货量x(件)之间的函数关系式;
(3)在(2)的条件下已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
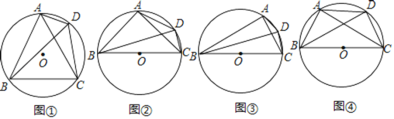
【题目】(1)方法选择:如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.
小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…
小军认为可用补短法证明:延长CD至点N,使得DN=AD…
请你选择一种方法证明.
(2)类比探究:(探究1)如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.
(探究2)如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是 .
(3)拓展猜想:如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】澜鑫商场为“双十一购物节”请甲乙两个广告公司布置展厅,已知乙单独完成此项任务的天数是甲单独完成此任务天数的2倍.若两公司合作4天,再由甲公司单独做3天就可以完成任务.
(1)甲公司与乙公司单独完成这项任务各需多少天?
(2)甲公司每天所需费用为5万元,乙公司每天所需费用为2万元,要使这项工作的总费用不超过40万元,则甲公司至多工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
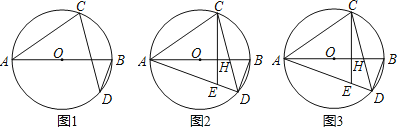
【题目】如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)若∠ABD=α,求∠BDC(用α表示);
(2)过点C作CE⊥AB于H,交AD于E,∠CAD=β,求∠ACE(用β表示);
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com