
【题目】某学校为了防控新型冠状病毒,购买了甲、乙两种消毒液进行校园环境消毒.己知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元.
(1)每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元?
(2)学校准备第三次购买这两种消毒液,其中甲种消毒液比乙种消毒液多10瓶,并且总花费不超过3 500元,最多能购买多少瓶甲种消毒液?
【答案】(1)每瓶甲种消毒液的价格是30元,每瓶乙种消毒液的价格是40元;(2)最多能购买甲种消毒液55瓶.
【解析】
(1)设每瓶甲种消毒液的价格是x元,每瓶乙种消毒液的价格是y元,根据“第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元”列出方程组求解即可;
(2)设可以购买甲种消毒液a瓶,根据“总花费不超过3 500元”列出不等式求解即可.
解:(1)设每瓶甲种消毒液的价格是x元,每瓶乙种消毒液的价格是y元.
依题意得:![]()
解得:![]() .
.
答:每瓶甲种消毒液的价格是30元,每瓶乙种消毒液的价格是40元.
(2)设可以购买甲种消毒液a瓶,则购买乙种消毒液(a-10)瓶.
依题意得:30a+40(a-10)≤3500.
解得:a≤![]()
∴a的最大整数解为55.
答:最多能购买甲种消毒液55瓶.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
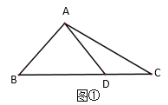
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
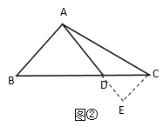
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
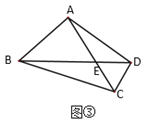
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解全校2000名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,将调查得到的结果绘制成如图所示的统计图和频数表(均不完整).
到校方式 | 频数 | 频率 |
自行车 | 24 | 0.3 |
步行 | ||
公交车 | 0.325 | |
私家车 | 10 | |
其他 | 4 |
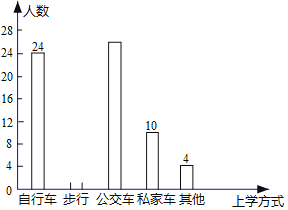
由图表中给出的信息回答下列问题:
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图.
(3)估计全校所有学生中有多少人步行上学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若![]() =-a,则a≤0;②若a>
=-a,则a≤0;②若a>![]() ,则a2>b2;③两个位似图形一定是相似图形;④平行四边形的两组对边分别相等.其中原命题与逆命题均为真命题的个数是( )
,则a2>b2;③两个位似图形一定是相似图形;④平行四边形的两组对边分别相等.其中原命题与逆命题均为真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它由四个全等的直角三角形拼接而成.点E,F,G,H分别是AF,BG,CH,DE的中点,点M,N,P,Q分别是HE,EF,FG,GH上的中点,且四边形MNPQ是正方形,已知正方形ABCD的面积为20,则正方形MNPQ的面积是( ).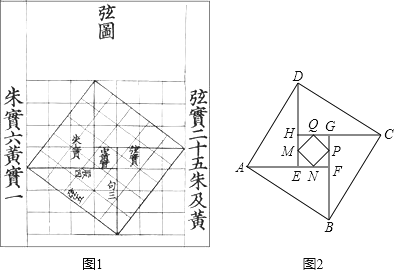
A.2B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图:
已知:直线l和l外一点P.

求作:直线l的垂线,使它经过点P.
做法:如图:(1)在直线l上任取两点A、B;
(2)分别以点A、B为圆心,![]() 、
、![]() 长为半径画弧,两弧相交于点Q;
长为半径画弧,两弧相交于点Q;
(3)作直线![]() .
.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是__________________.
(2)已知:直线l和l外一点P.
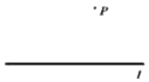
求作:![]() ,使它与直线l相切于点C(尺规作图,不写作法,保留作图痕迹).
,使它与直线l相切于点C(尺规作图,不写作法,保留作图痕迹).
(3)完成下面的证明.
证明:∵![]() _____________,且
_____________,且![]() ___________.
___________.
∴直线l是P的切线(_____________________)(填推理的依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com