
为了增加农民收入,村委会成立了蘑菇产销联合公司,小明家是公司成员之一,他家五月份收获干平菇42.5kg,干香菇35.5kg,按公司收购要求,需将两种磨菇包装成简装型和精装型两种型号的盒装蘑菇共60盒卖给公司,设包装简装型的盒数为x(盒),两种型号的盒装磨菇可获得总利润为y(元),包装要求及每盒获得的利润见下表:

(1)求y与x的函数关系式;
(2)为满足公司的收购要求,问有哪几种包装方案可供选择?并说明理由;
(3)小明的爸爸想只用这次的收入买一台价值1088元的包装机用于扩大再生产,你说能行吗?请说明你的理由.
|
(1) y=14x +24(60-x),y=1440-10x.(2) 依题意小明家共收干平菇42.5kg,干香菇35.5kg,所以 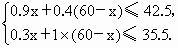
解之得 35≤x≤37.又x只能取整数,因此有三种方案:①60盒中35盒简装的,25盒精装的; ②60盒中36盒简装的,24盒精装的; ③60盒中37盒简装的,23盒精装的. (3) y=1440-10x.∵k=-10<0, ∴y随x的增大而减小. ∴当x=35时, 因此可以买包装机用于扩大再生产. |
|
本题考查的是运用函数知识解决实际问题,首先要审清题意,用含有自变量 x的代数式来表示y.(1) 简装型盒数为x盒,则精装型为(60-x)盒,简装型每盒利润14元,精装型每盒利润24元,则总利润=简装型利润+精装型利润,即y=14x+24(60-x);(2) 公司要求为简装型x盒,且每盒装入干平菇0.9kg和干香菇0.3kg,精装型(60-x)盒,且每盒装入干平菇0.4kg和干香菇1kg,而小明家共收获干平菇42.5kg,干香菇35.5kg,要想达到公司要求,必须使所有装入的干平菇≤42.5kg,所有装入的干香菇≤35.5kg,解不等式组可求出;(3) 运用函数增减性求最大值,并与1088比较大小或将上述方案分别代入函数表达式,求出对应的总利润,找出最大利润,与1088比较大小. |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
为了增加农民收入,村委会成立了蘑菇产销联合公司,小明家是公司成员之一,他家五月份收获干平菇42.5kg,干香菇35.5kg,按公司收购要求,需将两种磨菇包装成简装型和精装型两种型号的盒装蘑菇共60盒卖给公司,设包装简装型的盒数为x(盒),两种型号的盒装磨菇可获得总利润为y(元),包装要求及每盒获得的利润见下表:

(1)求y与x的函数关系式;
(2)为满足公司的收购要求,问有哪几种包装方案可供选择?并说明理由;
(3)小明的爸爸想只用这次的收入买一台价值1088元的包装机用于扩大再生产,你说能行吗?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 型号 品种及利润 | 装入干蘑菇重量(kg) | 装入干香菇重量(kg) | 每盒利润(元) |
| 简装型(每盒) | 0.9 | 0.3 | 14 |
| 精装版(每盒) | 0.4 | 1 | 24 |
查看答案和解析>>
科目:初中数学 来源:2012年沪科版中考数学摸拟试卷(解析版) 题型:解答题
| 型号 品种及利润 | 装入干蘑菇重量(kg) | 装入干香菇重量(kg) | 每盒利润(元) |
| 简装型(每盒) | 0.9 | 0.3 | 14 |
| 精装版(每盒) | 0.4 | 1 | 24 |
查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(8)(解析版) 题型:解答题
| 型号 品种及利润 | 装入干蘑菇重量(kg) | 装入干香菇重量(kg) | 每盒利润(元) |
| 简装型(每盒) | 0.9 | 0.3 | 14 |
| 精装版(每盒) | 0.4 | 1 | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com