
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过点C作AD的垂线,交AB于点F,求证∠ADC=∠BDE
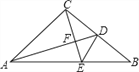
【答案】见解析
【解析】试题分析:作CH⊥AB于H交AD于P,根据已知条件和等腰直角三角形的性质易证△APH≌△CEH,可得PH=EH,再证得CP=EB,∠PCD=∠EBD=45°,DC=DB,即可得△PDC≌△EDB,结论得证.
试题解析:
作CH⊥AB于H交AD于P,
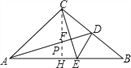
∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45.
∴∠HCB=90∠CBA=45=∠CBA.
又∵BC中点为D,
∴CD=BD.
又∵CH⊥AB,
∴CH=AH=BH.
又∵∠PAH+∠APH=90,∠PCF+∠CPF=90,∠APH=∠CPF,
∴∠PAH=∠ECH.
在△APH与△CEH中
∠PAH=∠ECH,AH=CH,∠PHA=∠EHC,
∴△APH≌△CEH(ASA).
∴PH=EH,
又∵PC=CHPH,BE=BHHE,
∴CP=EB.
∵△ACB是等腰直角三角形,
∴∠B=45,
即∠EBD=45,
∵CH⊥AB,
∴∠PCD=45=∠EBD,
在△PDC与△EDB中
PC=EB,∠PCD=∠EBD,DC=DB,
∴△PDC≌△EDB(SAS).
∴∠ADC=∠BDE.


科目:初中数学 来源: 题型:
【题目】某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评。结果如下表所示:


规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
综合得分=演讲答辩得分×(1-a)+民主测评得分×a(0.5≤a≤0.8);
(1) 当a=0.6时,甲的综合得分是多少?
(2) 如果以综合得分来确定班长,试问:甲、乙两位同学哪一位当选为班长?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1
(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.
(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为______,当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是______.
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2(a≥1)的图像上两点A、B的横坐标分别是-1、2,点O是坐标原点,如果△AOB是直角三角形,则△OAB的周长为 __ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某正方形的面积是(16-8x+x2)cm2(x>4),则该正方形的周长是
A. (4-x)cm B. (x-4)cm
C. (16-4x)cm D. (4x-16)cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com