
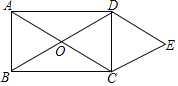
【题目】如图,矩形ABCD对角线AC、BD交于点O,边AB=6,AD=8,四边形OCED为菱形,若将菱形OCED绕点O旋转一周,旋转过程中OE与矩形ABCD的边的交点始终为M,则线段ME的长度可取的整数值为___________________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
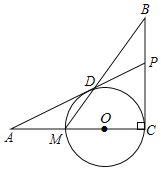
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是⊙O的切线;
(3)若AD=12,AM=MC,求PB和DM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
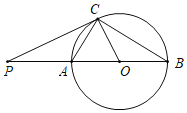
【题目】如图,已知AB是⊙O的直径,AC是弦,点P是BA延长线上一点,连接PC、BC,∠PCA=∠B.
(1)求证:PC是⊙O的切线;
(2)若PC=4,PA=2,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() 是
是![]() 上一点,点
上一点,点![]() 从点
从点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止;点
时停止;点![]() 从点
从点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,速度均为每秒1个单位长度.如果点
时停止,速度均为每秒1个单位长度.如果点![]() ,
,![]() 同时开始运动,设运动时间为
同时开始运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
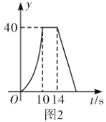
与![]() 的函数图象如图2所示,有以下结论:
的函数图象如图2所示,有以下结论:
①![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() 是等腰三角形;
是等腰三角形;
⑤当![]() 时,
时,![]() .
.
其中正确的有( ).

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
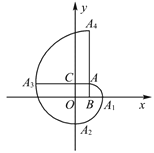
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,继续以点
为半径的圆弧,继续以点![]() 为圆心,按上述作法得到的曲线
为圆心,按上述作法得到的曲线![]() …,称为正方形的“渐开线”,则点
…,称为正方形的“渐开线”,则点![]() 的坐标是______.
的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象和性质.小奥根据学习函数的经验,对函数
的图象和性质.小奥根据学习函数的经验,对函数![]() 的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是_________;
的取值范围是_________;
(2)下表是![]() 与
与![]() 的几组对应值,则
的几组对应值,则![]() 的值为______,
的值为______,![]() 的值为______;
的值为______;
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
|
| 2 |
|
|
| … |
(3)如右图,在平面直角坐标系![]() 中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;
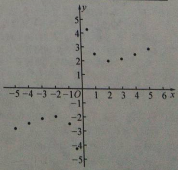
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是![]() .结合函数图象,写出该函数的其他两条性质:①_________,②_________.
.结合函数图象,写出该函数的其他两条性质:①_________,②_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com