
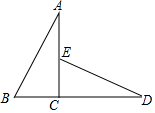
 如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.
如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm. 分析 首先确定∠CED=60°,再根据全等三角形的性质可得∠ECD=∠ACB=90°,进而可得∠D的度数,然后再根据三角函数可得EC的长,然后可得AE的长.
解答 解:∵∠AED=120°,
∴∠CED=60°,
∵△ABC≌△DEC,
∴∠ACB=∠ECD=90°,
∵∠ACB+∠ECD=180°,
∴∠ECD=∠ACB=90°,
∴∠D=30°,
∵CD=2$\sqrt{3}$cm,
∴EC=CD•tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
∵△ABC≌△DEC,
∴AC=CD=2$\sqrt{3}$cm,
∴AE=AC-CE=2$\sqrt{3}$-2(cm),
故答案为:30;(2$\sqrt{3}$-2).
点评 此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等,全等三角形的对应角相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
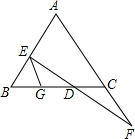 如图,已知EG∥AF,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只需写出一种情况)
如图,已知EG∥AF,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只需写出一种情况)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ﹒1个 | B. | ﹒2个 | C. | ﹒3个 | D. | ﹒4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com