
【题目】如图,等边![]() 的边长为5,点
的边长为5,点![]() 在
在![]() 边上,点
边上,点![]() 为
为![]() 延长线一点,连结
延长线一点,连结![]() 交
交![]() 于
于![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 边上,当
边上,当![]() 时,
时,![]() 的长为( )
的长为( )
A.1.5B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
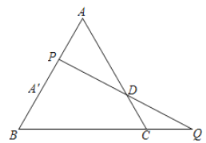
过P作PM∥BC交AC于M,证出△APM为等边三角形,得出PA=PM=AM,证明△PMD≌△QCD (AAS)得出PD=QD,证明△AA D是等边三角形,得出∠AAD=60°=∠B,证出AD// BC,得出AB=PA=PA,即可得出答案.
解:过P作PM// BC交AC于M,如图所示:

∵三边形ABC是等边三角形,
∴∠A=∠B=∠ACB=60° ,PM // BC,
∴∠APM= ∠ B=60°,∠AMP=∠ACB=60°,∠PMD=∠QCD,
∴△APM为等边三角形
∴PA=PM= AM,
∵PA=CQ ,
∴ PM=CQ ,
在△PMD和△QCD中,
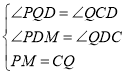
∴△PMD≌△QCD (AAS)
∴PD=QD,
∵点A关于直线PQ的对称点A恰好落在AB边上,
∴PA=PA,∠APD=90° ,
∴∠ADP=30°
∴AP=![]() AD,
AD,
∵PA=AM
∴AA=AD,PA=MD
△AAD是等边三角形,
∴∠AAD=60°=∠B,
∴AD// BC,
∴PD=QD,
∴AB=PA=PA,
∴AB=![]() AB=
AB=![]()
故选:C


科目:初中数学 来源: 题型:
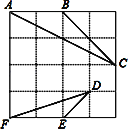
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
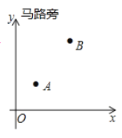
【题目】要在马路边设一个共享单车投放点,向![]() 两家公司提供服务,投放点应设在什么地方,才能使从
两家公司提供服务,投放点应设在什么地方,才能使从![]() 到它的距离之和最短?小明根据实际情况,以马路为
到它的距离之和最短?小明根据实际情况,以马路为![]() 轴建立了如图所示的平面直角坐标系,
轴建立了如图所示的平面直角坐标系,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,则从
,则从![]() 两点到投放点距离之和的最小值是__________,投放点的坐标是__________.
两点到投放点距离之和的最小值是__________,投放点的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
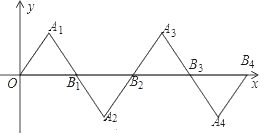
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B20A21B21的顶点A21的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
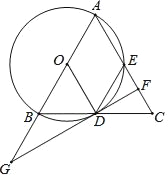
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC,AC于D,E两点,过点D作⊙O的切线,交AC于点F,交AB的延长线于点G.
(1)求证:EF=CF;
(2)若cos∠ABC=![]() ,AB=10,求线段AF的长.
,AB=10,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座石拱桥的桥拱是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.
为半径的一段圆弧.

![]() 请你确定弧
请你确定弧![]() 的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
![]() 如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为
如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为![]() 米,拱高(即弧的中点到弦的距离)为
米,拱高(即弧的中点到弦的距离)为![]() 米,求桥拱所在圆的半径.
米,求桥拱所在圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com