
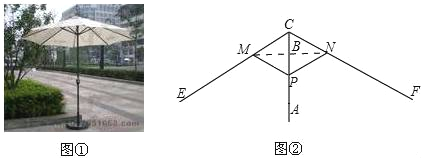
”¾ĢāÄæ”æĶ¼1ĖłŹ¾µÄÕŚŃōÉ”£¬É”±ś“¹Ö±ÓŚĖ®Ę½µŲĆę£¬ĘäŹ¾ŅāĶ¼ČēĶ¼2”¢µ±É”ŹÕ½ōŹ±£¬µćPÓėµćAÖŲŗĻ£»µ±É”ĀżĀż³ÅæŖŹ±£¬¶ÆµćPÓÉAĻņBŅĘ¶Æ£»µ±µćPµ½“ļµćBŹ±£¬É”ÕŵĆ×īæŖ”¢ŅŃÖŖÉ”ŌŚ³ÅæŖµÄ¹ż³ĢÖŠ£¬×ÜÓŠPM=PN=CM=CN=6.0·ÖĆ×£¬CE=CF=18.0·ÖĆ×£¬BC=2.0·ÖĆ×”¢ÉčAP=x·ÖĆ×£®
£Ø1£©ĒóxµÄȔֵ·¶Ī§£»
£Ø2£©Čō”ĻCPN=60”ć£¬ĒóxµÄÖµ£»
£Ø3£©ÉčŃō¹āÖ±ÉäĻĀ£¬É”ĻĀµÄŅõÓ°£Ø¼Ł¶ØĪŖŌ²Ćę£©Ć껿ĪŖy£¬Ēóy¹ŲÓŚxµÄ¹ŲĻµŹ½£Ø½į¹ū±£Įō¦Š£©£®
”¾“š°ø”æ£Ø1£©0”Üx”Ü10£»£Ø2£©x=6£»£Ø3£©y=©![]() ¦Šx2+54¦Šx£®
¦Šx2+54¦Šx£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅā£¬µĆAC=CN+PN£¬½ųŅ»²½ĒóµĆABµÄ³¤£¬¼“æÉĒóµĆxµÄȔֵ·¶Ī§£»
£Ø2£©øł¾ŻµČ±ßČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ¼“æÉĒó½ā£»
£Ø3£©Į¬½ÓMN”¢EF£¬·Ö±š½»ACÓŚB”¢H£®“ĖĢāøł¾ŻĮāŠĪCMPNµÄŠŌÖŹĒóµĆMBµÄ³¤£¬ŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄ¶ŌÓ¦±ßµÄ±ČĻąµČ£¬ĒóµĆŌ²µÄ°ė¾¶¼“æÉ£®
£Ø1£©”ßBC=2·ÖĆ×£¬AC=CN+PN=12·ÖĆ×£¬
”ąAB=AC©BC=10·ÖĆ×£¬
”ąxµÄȔֵ·¶Ī§ŹĒ£ŗ0”Üx”Ü10£»
£Ø2£©”ßCN=PN£¬”ĻCPN=60”ć£¬
”ą”÷PCNŹĒµČ±ßČż½ĒŠĪ£¬
”ąCP=6·ÖĆ×£¬
”ąAP=AC©PC=6·ÖĆ×£¬
¼“µ±”ĻCPN=60”揱£¬x=6£»
£Ø3£©Į¬½ÓMN”¢EF£¬·Ö±š½»ACÓŚB”¢H£¬
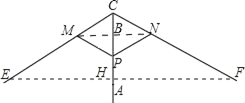
”ßPM=PN=CM=CN£¬
”ąĖıߊĪPNCMŹĒĮāŠĪ£¬
”ąMNÓėPC»„Ļą“¹Ö±Ę½·Ö£¬ACŹĒ”ĻECFµÄĘ½·ÖĻߣ¬
PB=![]() =6-
=6-![]() £¬
£¬
ŌŚRt”÷MBPÖŠ£¬PM=6·ÖĆ×£¬
”ąMB2=PM2©PB2=62©£Ø6©![]() x£©2=6x©
x£©2=6x©![]() x2£®
x2£®
”ßCE=CF£¬ACŹĒ”ĻECFµÄĘ½·ÖĻߣ¬
”ąEH=HF£¬EF”ĶAC£¬
”ß”ĻECH=”ĻMCB£¬”ĻEHC=”ĻMBC=90”ć£¬
”ą”÷CMB”×”÷CEH£¬
”ą![]() =
=![]() £¬
£¬
”ą![]() £¬
£¬
”ąEH2=9MB2=9£Ø6x©![]() x2£©£¬
x2£©£¬
”ąy=¦ŠEH2=9¦Š£Ø6x©![]() x2£©£¬
x2£©£¬
¼“y=©![]() ¦Šx2+54¦Šx£®
¦Šx2+54¦Šx£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
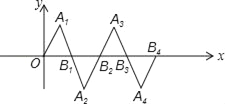
”¾ĢāÄæ”æŌŚČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷OA1B1ŹĒ±ß³¤ĪŖ2µÄµČ±ßČż½ĒŠĪ£¬×÷”÷B2A2B1Óė”÷OA1B1¹ŲÓŚµćB1³ÉÖŠŠÄ¶Ō³Ę£¬ŌŁ×÷”÷B2A3B3Óė”÷B2A2B1¹ŲÓŚµćB2³ÉÖŠŠÄ¶Ō³Ę£¬Čē“Ė×÷ĻĀČ„£¬Ōņ”÷B2nA2n+1B2n+1£ØnŹĒÕżÕūŹż£©µÄ¶„µćA2n+1µÄ×ų±źŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ¼ÓĒæѧɜµÄ°²Č«ŅāŹ¶£¬Ä³Š£×éÖÆĮĖѧɜ²Ī¼Ó°²Č«ÖŖŹ¶¾ŗČü£¬“ÓÖŠ³éČ”ĮĖ²æ·Öѧɜ³É¼Ø£ØµĆ·ÖŹżČ”Õż
ÕūŹż£¬Āś·ÖĪŖ![]() ·Ö£©½ųŠŠĶ³¼Ę£¬ŅŃÖŖ
·Ö£©½ųŠŠĶ³¼Ę£¬ŅŃÖŖ![]() ×éµÄʵŹż
×éµÄʵŹż![]() ±Č
±Č![]() ×éµÄʵŹż
×éµÄʵŹż![]() Š”£¬»ęÖĘĶ³¼ĘʵŹż·Ö±šÖ±·½Ķ¼£ØĪ“Ķź³É£©
Š”£¬»ęÖĘĶ³¼ĘʵŹż·Ö±šÖ±·½Ķ¼£ØĪ“Ķź³É£©
ŗĶÉČŠĪĶ³¼ĘĶ¼ČēĻĀ£¬
Ēė½ā“šĻĀĮŠĪŹĢā£ŗ
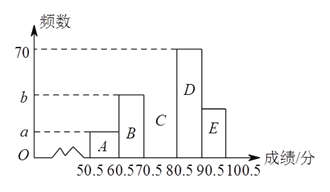
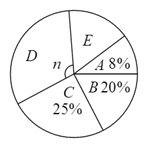
£Ø![]() £©Ńł±¾ČŻĮæĪŖ£ŗ__________£¬
£©Ńł±¾ČŻĮæĪŖ£ŗ__________£¬ ![]() ĪŖ__________£®
ĪŖ__________£®
£Ø![]() £©
£©![]() ĪŖ__________£¬
ĪŖ__________£¬ ![]() ×éĖłÕ¼±ČĄżĪŖ__________
×éĖłÕ¼±ČĄżĪŖ__________![]() £®
£®
£Ø![]() £©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£®
£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£®
£Ø![]() £©Čō³É¼ØŌŚ
£©Čō³É¼ØŌŚ![]() ·ÖŅŌÉĻ¼Ē×÷ÓÅŠć£¬Č«Š£¹²ÓŠ
·ÖŅŌÉĻ¼Ē×÷ÓÅŠć£¬Č«Š£¹²ÓŠ![]() Ćūѧɜ£¬¹Ą¼Ę³É¼ØÓÅŠćѧɜӊ__________Ćū£®
Ćūѧɜ£¬¹Ą¼Ę³É¼ØÓÅŠćѧɜӊ__________Ćū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£ØŌĶĮĄķ½ā£©ĄūÓĆĶźČ«Ę½·½¹«Ź½£¬æÉŅŌ½«¶ąĻīŹ½![]() ±äŠĪĪŖ
±äŠĪĪŖ![]() µÄŠĪŹ½£¬ĪŅĆĒ°ŃÕāŃłµÄ±äŠĪ·½·Ø½Š×ö¶ąĻīŹ½
µÄŠĪŹ½£¬ĪŅĆĒ°ŃÕāŃłµÄ±äŠĪ·½·Ø½Š×ö¶ąĻīŹ½![]() µÄÅä·½·Ø£®ŌĖÓƶąĻīŹ½µÄÅä·½·Ø¼°Ę½·½²ī¹«Ź½ÄܶŌŅ»Š©¶ąĻīŹ½½ųŠŠ·Ö½āŅņŹ½£®
µÄÅä·½·Ø£®ŌĖÓƶąĻīŹ½µÄÅä·½·Ø¼°Ę½·½²ī¹«Ź½ÄܶŌŅ»Š©¶ąĻīŹ½½ųŠŠ·Ö½āŅņŹ½£®
ĄżČē£ŗ![]()
![]()
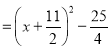
![]()
![]()
£ØĪŹĢā½ā¾ö£©øł¾ŻŅŌÉĻ²ÄĮĻ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ÓƶąĻīŹ½µÄÅä·½·Ø½«¶ąĻīŹ½![]() »Æ³É
»Æ³É![]() µÄŠĪŹ½£»
µÄŠĪŹ½£»
£Ø2£©ÓƶąĻīŹ½µÄÅä·½·Ø¼°Ę½·½²ī¹«Ź½¶Ō¶ąĻīŹ½![]() ½ųŠŠ·Ö½āŅņŹ½£»
½ųŠŠ·Ö½āŅņŹ½£»
£Ø3£©ĒóÖ¤£ŗ²»ĀŪ![]() £¬
£¬![]() Č”ČĪŗĪŹµŹż£¬¶ąĻīŹ½
Č”ČĪŗĪŹµŹż£¬¶ąĻīŹ½![]() µÄÖµ×ÜĪŖÕżŹż£®
µÄÖµ×ÜĪŖÕżŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°Ź®×ÖĻą³Ė·Ø”±ÄܰѶž“ĪČżĻīŹ½·Ö½āŅņŹ½£¬¶ŌÓŚŠĪČēax2+bxy+cy2µÄ¹ŲÓŚx£¬yµÄ¶ž“ĪČżĻīŹ½Ą“Ėµ£¬·½·ØµÄ¹Ų¼üŹĒ°Ńx2ĻīĻµŹża·Ö½ā³ÉĮ½øöŅņŹża1£¬a2µÄ»ż£¬¼“a£½a1a2£¬°Ńy2ĻīĻµŹżc·Ö½ā³ÉĮ½øöŅņŹżc1£¬c2µÄ»ż£¬¼“c£½c1c2£¬²¢Ź¹a1c2+a2c1ÕżŗƵČÓŚxyĻīµÄĻµŹżb£¬ÄĒĆ“æÉŅŌÖ±½ÓŠ“³É½į¹ū£ŗax2+bxy+cy2£½£Øa1x+c1y£©£Øa2x+c2y£©£®
Ąż£ŗ·Ö½āŅņŹ½£ŗx2©2xy©8y2£®
½ā£ŗČēĶ¼1£¬ĘäÖŠ1£½1”Į1£¬©8£½£Ø©4£©”Į2£¬¶ų©2£½1”Į2+1”Į£Ø©4£©£®
”ąx2©2xy©8y2£½£Øx©4y£©£Øx+2y£©
¶ų¶ŌÓŚŠĪČēax2+bxy+cy2+dx+ey+fµÄx£¬yµÄ¶žŌŖ¶ž“ĪŹ½Ņ²æÉŅŌÓĆŹ®×ÖĻą³Ė·ØĄ“·Ö½ā£¬ČēĶ¼2£¬½«a·Ö½ā³Émn³Ė»ż×÷ĪŖŅ»ĮŠ£¬c·Ö½ā³Épq³Ė»ż×÷ĪŖµŚ¶žĮŠ£¬f·Ö½ā³Éjk³Ė»ż×÷ĪŖµŚČżĮŠ£¬Čē¹ūmq+np£½b£¬pk+qj£½e£¬mk+nj£½d£¬¼“µŚ1£¬2ĮŠ”¢µŚ2£¬3ĮŠŗĶµŚ1£¬3ĮŠ¶¼Āś×揮×ÖĻą³Ė¹ęŌņ£¬ŌņŌŹ½£½£Ømx+py+j£©£Ønx+qy+k£©£»
Ąż£ŗ·Ö½āŅņŹ½£ŗx2+2xy©3y2+3x+y+2
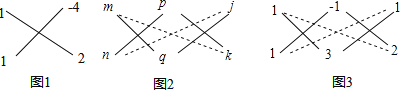
½ā£ŗČēĶ¼3£¬ĘäÖŠ1£½1”Į1£¬©3£½£Ø©1£©”Į3£¬2£½1”Į2£»
¶ų2£½1”Į3+1”Į£Ø©1£©£¬1£½£Ø©1£©”Į2+3”Į1£¬3£½1”Į2+1”Į1£»
”ąx2+2xy©3y2+3x+y+2£½£Øx©y+1£©£Øx+3y+2£©
ĒėĶ¬Ń§ĆĒĶعżŌĶĮÉĻŹö²ÄĮĻ£¬Ķź³ÉĻĀĮŠĪŹĢā£ŗ
£Ø1£©·Ö½āŅņŹ½£ŗ
¢Ł6x2©17xy+12y2£½”” ””
¢Ś2x2©xy©6y2+2x+17y©12£½”” ””
¢Ūx2©xy©6y2+2x©6y£½”” ””
£Ø2£©Čō¹ŲÓŚx£¬yµÄ¶žŌŖ¶ž“ĪŹ½x2+7xy©18y2©5x+my©24æÉŅŌ·Ö½ā³ÉĮ½øöŅ»“ĪŅņŹ½µÄ»ż£¬ĒómµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖµćA£Ø0£¬3£©£¬µćB£Ø![]() £¬0£©£¬Į¬½ÓAB£¬Čō¶ŌÓŚĘ½ĆęÄŚŅ»µćC£¬µ±”÷ABCŹĒŅŌABĪŖŃüµÄµČŃüČż½ĒŠĪŹ±£¬³ĘµćCŹĒĻ߶ĪABµÄ”°µČ³¤µć”±£®
£¬0£©£¬Į¬½ÓAB£¬Čō¶ŌÓŚĘ½ĆęÄŚŅ»µćC£¬µ±”÷ABCŹĒŅŌABĪŖŃüµÄµČŃüČż½ĒŠĪŹ±£¬³ĘµćCŹĒĻ߶ĪABµÄ”°µČ³¤µć”±£®
£Ø1£©ŌŚµćC1£Ø©2£¬3+2![]() £©£¬µćC2£Ø0£¬©2£©£¬µćC3£Ø3+
£©£¬µćC2£Ø0£¬©2£©£¬µćC3£Ø3+![]() £¬©
£¬©![]() £©ÖŠ£¬Ļ߶ĪABµÄ”°µČ³¤µć”±ŹĒµć________£»
£©ÖŠ£¬Ļ߶ĪABµÄ”°µČ³¤µć”±ŹĒµć________£»
£Ø2£©ČōµćD£Øm£¬n£©ŹĒĻ߶ĪABµÄ”°µČ³¤µć”±£¬ĒŅ”ĻDAB=60”ć£¬ĒóµćDµÄ×ų±ź£»
£Ø3£©ČōÖ±Ļßy=kx+3![]() kÉĻÖĮÉŁ“ęŌŚŅ»øöĻ߶ĪABµÄ”°µČ³¤µć”±£¬ĒókµÄȔֵ·¶Ī§£®
kÉĻÖĮÉŁ“ęŌŚŅ»øöĻ߶ĪABµÄ”°µČ³¤µć”±£¬ĒókµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
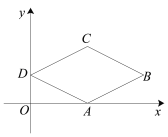
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĖıߊĪABCDŹĒĮāŠĪ£¬ĘäÖŠBµć×ų±źŹĒ(8£¬2)£¬Dµć×ų±źŹĒ(0£¬2)£¬µćAŌŚxÖįÉĻ£¬ŌņĮāŠĪABCDµÄÖܳ¤ŹĒ£Ø £©
A.2![]()
B.8
C.8![]()
D.12
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬AB=BD£¬µćE”¢F·Ö±šŹĒAB”¢ADÉĻČĪŅāµÄµć£Ø²»Óė¶ĖµćÖŲŗĻ£©£¬ĒŅAE=DF£¬Į¬½ÓBFÓėDEĻą½»ÓŚµćG£¬Į¬½ÓCGÓėBDĻą½»ÓŚµćH£®øų³öČēĻĀ¼øøö½įĀŪ£ŗ¢Ł”÷AED”Õ”÷DFB£»¢ŚSĖıߊĪBCDG=![]() £»¢ŪČōAF=2DF£¬ŌņBG=6GF£»¢ÜCGÓėBDŅ»¶Ø²»“¹Ö±£»¢Ż”ĻBGEµÄ“óŠ”ĪŖ¶ØÖµ£®
£»¢ŪČōAF=2DF£¬ŌņBG=6GF£»¢ÜCGÓėBDŅ»¶Ø²»“¹Ö±£»¢Ż”ĻBGEµÄ“óŠ”ĪŖ¶ØÖµ£®
ĘäÖŠÕżČ·µÄ½įĀŪøöŹżĪŖ£Ø £©

A. 4 B. 3 C. 2 D. 1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
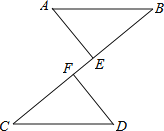
”¾ĢāÄæ”æČēĶ¼£¬AB”ĪCD£¬AB=CD£¬µćE”¢FŌŚBCÉĻ£¬ĒŅBF=CE£®
£Ø1£©ĒóÖ¤£ŗ”÷ABE”Õ”÷DCF£»
£Ø2£©ŹŌÖ¤Ć÷£ŗŅŌA”¢F”¢D”¢EĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com