
| 1 |
| 2 |
| 1 |
| 2 |
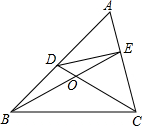 述条件的图形中是否存在等对边四边形,并证明你的结论.
述条件的图形中是否存在等对边四边形,并证明你的结论. 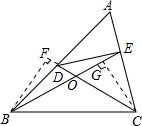 解:(1)回答正确的给(1分)(如:平行四边形、等腰梯形等).
解:(1)回答正确的给(1分)(如:平行四边形、等腰梯形等).| 1 |
| 2 |
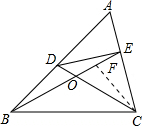
| 1 |
| 2 |
|


科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:
 我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
1.请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
2.如图,在![]() 中,点
中,点![]() 分别在
分别在 上,设
上,设![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() .请你写出图中一个与
.请你写出图中一个与![]() 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;
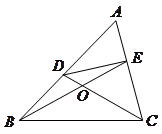
3.在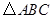 中,如果
中,如果 是不等于
是不等于 的锐角,点
的锐角,点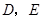 分别在
分别在 上,且
上,且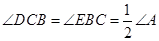 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽合肥市古都中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
【小题1】请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
【小题2】如图,在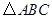 中,点
中,点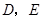 分别在
分别在 上,设
上,设 相交于点
相交于点 ,若
,若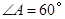 ,
, .请你写出图中一个与
.请你写出图中一个与 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;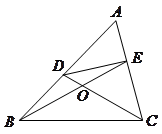
【小题3】在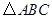 中,如果
中,如果 是不等于
是不等于 的锐角,点
的锐角,点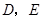 分别在
分别在 上,且
上,且 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com