
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 过
过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
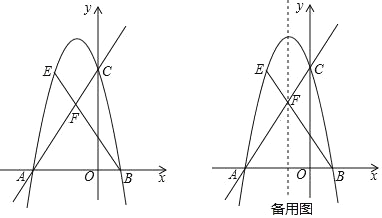
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在直线![]() 上方的抛物线上是否存在点
上方的抛物线上是否存在点![]() ,使
,使![]() 与
与![]() 的交点
的交点![]() 恰好为
恰好为![]() 的中点?如果存在,求出点
的中点?如果存在,求出点![]() 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
(3)若点![]() 在抛物线上且横坐标为
在抛物线上且横坐标为![]() ,点
,点![]() 是抛物线对称轴上一点,在抛物线上存在一点
是抛物线对称轴上一点,在抛物线上存在一点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?直接写出点
为顶点的四边形是平行四边形?直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(1,0) (2)不存在;答案见解析 (3)
;(1,0) (2)不存在;答案见解析 (3)![]() 或
或![]() 或
或![]()
【解析】
(1)先根据直线![]() 求出点A、C的坐标,再将点A、C的坐标代入抛物线
求出点A、C的坐标,再将点A、C的坐标代入抛物线![]() ,解方程组求得b、c的值即可得抛物线解析式,令
,解方程组求得b、c的值即可得抛物线解析式,令![]()
解方程即可点B的坐标;
(2)先假设点![]() 存在,设点
存在,设点![]() ,再过点
,再过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() 易知
易知![]() ,且
,且![]() ,继而可求得点F的坐标,由EH=2FG,
,继而可求得点F的坐标,由EH=2FG,![]() ,判定方程有无实数根即可判断是否存在点E,使
,判定方程有无实数根即可判断是否存在点E,使![]() 与
与![]() 的交点
的交点![]() 恰好为
恰好为![]() 的中点;
的中点;
(3)先求得点E的坐标和点N的横坐标,再分EB为平行四边形的边和EB为平行四边形的对角线两种情况,其中EB为平行四边形的边时,再分点M在对称轴右侧和左侧两种情况分别求解可得.
解:(1)在![]() 中,当
中,当![]() 时
时![]()
当![]() 时
时![]()
![]()
![]() 抛物线
抛物线![]() 的图象经过
的图象经过![]() 两点,
两点,
![]() ,
,
解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
令![]()
解得![]()
![]() ;
;
(2)不存在点![]() 使点
使点![]() 为
为![]() 的中点,
的中点,
理由是:如果点![]() 存在,设点
存在,设点![]() 的横坐标为
的横坐标为![]()
![]()
如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]()
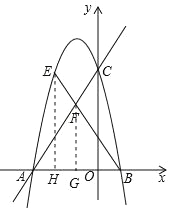
则![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,
∵EH=2FG,
![]() ,
,
![]()
![]()
![]() 方程无实数根,
方程无实数根,
![]() 满足条件的
满足条件的![]() 点不存在;
点不存在;
(3)![]() 或
或![]() 或
或![]()
![]() 点
点![]() 在对称轴上,
在对称轴上,
![]() ,
,
将![]() 代入
代入![]()
得:![]() ,
,
![]() ,
,
①当![]() 为平行四边形的边时,分两种情况:
为平行四边形的边时,分两种情况:
![]() 点
点![]() 在对称轴右侧时,
在对称轴右侧时,![]() 为对角线,
为对角线,
![]() ,
,
![]()
当![]() 时,
时,![]()
![]() ;
;
![]() 点
点![]() 在对称轴左侧时,
在对称轴左侧时,![]() 为对角线,
为对角线,
![]() ,
,
![]()
当![]() 时,
时,![]()
![]() ,
,
②当![]() 为平行四边形的对角线时,
为平行四边形的对角线时,
![]()
![]() ,
,
![]()
当![]() 时,
时,![]()
![]() ;
;
综上所述,![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,MN与边AD交于点E.
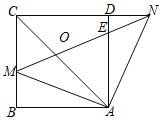
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE;
(3)MN和AC相交于O点,若BM=1,AB=3,试猜想线段OM,ON的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C'落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C'落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
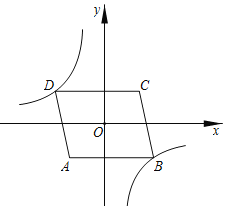
A.24B.20C.18D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
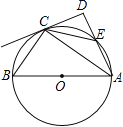
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,过点A作AD⊥CD于点D,交⊙O于点E,且![]() =
=![]() .
.
(1)求证:CD是⊙O的切线;
(2)若tan∠CAB=![]() ,BC=3,求DE的长.
,BC=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在参加了全市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度“阅读素养、数学素养、科学素养、人文素养”,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).小明、小颖和小雯在协助老师进行统计后,有这样一段对话:
小明:“选科学素养和人文素养的同学分别为![]() 人,
人,![]() 人.”
人.”
小颖:“选数学素养的同学比选阅读素养的同学少![]() 人.”
人.”
小雯:“选科学素养的同学占样本总数的![]() .”
.”
(1)这次抽样调查了多少名学生?
(2)样本总数中,选“阅读素养”、“数学素养”的学生各多少人?
(3)如图是调查结果整理后绘制成的扇形图.请直接在横线上补全相关百分比,并求出“数学素养”所对应的圆心角度数;
(4)该校八年级有学生![]() 人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?
人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?
[Failed to download image : blob:http://qbm.xkw.com/61c6a1d7-da76-4939-b41e-e8015f4fdd80]
查看答案和解析>>
科目:初中数学 来源: 题型:
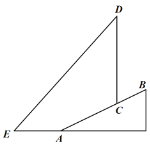
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,点
轴对称,点![]() 是
是![]() 轴上一点,将函数
轴上一点,将函数![]() 的图象位于直线
的图象位于直线![]() 左侧的部分,以
左侧的部分,以![]() 轴为对称轴翻折,得到新的函数
轴为对称轴翻折,得到新的函数![]() 的图象,我们称函数
的图象,我们称函数![]() 是函数
是函数![]() 的对称折函数,函数
的对称折函数,函数![]() 的图象记作
的图象记作![]() ,函数
,函数![]() 的图象位于直线
的图象位于直线![]() 上以及右侧的部分记作
上以及右侧的部分记作![]() ,图象
,图象![]() 和
和![]() 合起来记作图象
合起来记作图象![]() .
.
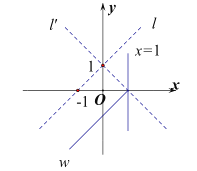
例如:如图,函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的对称折函数
时,它的对称折函数![]() 的解析式为
的解析式为![]() .
.
(1)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的对称折函数
时,它的对称折函数![]() 的解析式为_______;
的解析式为_______;
(2)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 且
且![]() 时,求图象
时,求图象![]() 上点的纵坐标的最大值和最小值;
上点的纵坐标的最大值和最小值;
(3)函数![]() 的解析式为
的解析式为![]() .若
.若![]() ,直线
,直线![]() 与图象
与图象![]() 有两个公共点,求
有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 轴上的点,且
轴上的点,且![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 轴正半轴上的任意一点,连结
轴正半轴上的任意一点,连结![]() ,以
,以![]() 为边按顺时针方向作正方形
为边按顺时针方向作正方形![]() .
.

(1)填空:点![]() 的坐标为______;
的坐标为______;
(2)记正方形![]() 的面积为
的面积为![]() ,①求
,①求![]() 关于
关于![]() 的函数关系式;②当
的函数关系式;②当![]() 时,求
时,求![]() 的值.
的值.
(3)是否存在满足条件的![]() 的值,使正方形的顶点
的值,使正方形的顶点![]() 或
或![]() 落在
落在的边上?若存在,求出所有满足条件的
![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com