
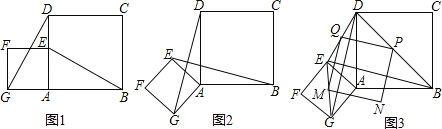
【题目】如图1所示,四边形AEFG与四边形ABCD是正方形,其中G、A、B三点在同一直线上.连接DG、BE.完成下面问题:
(1)求证:BE=DG;
(2)如图2,将正方形AEFG绕点A逆时针转过一定角度时,小明发现:BE=DG且BE⊥DG,请你帮助小明证明这两个结论;
(3)如图3,小明还发现:在旋转过程中,分别连接EG、GB、BD、DE的中点,得到的四边形MNPQ是正方形.若AB=a,AE=b其中a>b,你能帮小明求出正方形MNPQ的面积的范围吗?写出过程.
【答案】(1)见解析;(2)见解析;(3)![]() (a﹣b)2≤正方形MNPQ的面积≤
(a﹣b)2≤正方形MNPQ的面积≤![]() (a+b)2.
(a+b)2.
【解析】
试题分析:(1)根据正方形的性质得到AD=AB,AE=AG,∠DAG=∠BAE=90°,证明△DAG≌△BAE,根据全等三角形的性质证明结论;
(2)根据全等三角形的性质和互余的概念以及垂直的定义证明即可;
(3)根据三角形中位线定理得到MN=![]() BE,根据旋转的性质和正方形的面积公式计算即可.
BE,根据旋转的性质和正方形的面积公式计算即可.
(1)证明:∵四边形AEFG与四边形ABCD是正方形,
∴AD=AB,AE=AG,∠DAG=∠BAE=90°,
在△DAG和△BAE中,
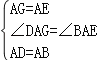 ,
,
∴△DAG≌△BAE,
∴BE=DG;
(2)证明:如图2,∵∠EAG=∠BAD=90°,
∴∠DAG=∠BAE,
在△DAG和△BAE中,
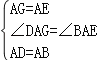 ,
,
∴△DAG≌△BAE,
∴BE=DG,∠ADG=∠ABE,
∵∠ABE+∠AHB=90°,∠AHB=∠DHE,
∴∠ADG+∠DHE=90°,
∴BE⊥DG,
∴BE=DG且BE⊥DG;
(3)解:∵M、N分别是EG、GB的中点,
∴MN=![]() BE,
BE,
∴当BE最小时,正方形MNPQ是面积最小,BE最大时,正方形MNPQ是面积最大,
由题意可知,当点E旋转到线段AB上时,BE最小为a﹣b,
当点E旋转到线段AB的延长线上时,BE最答为a+b,
∴![]() (a﹣b)2≤正方形MNPQ的面积≤
(a﹣b)2≤正方形MNPQ的面积≤![]() (a+b)2.
(a+b)2.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,该抛物线顶点为D,对称轴交x轴于点H.
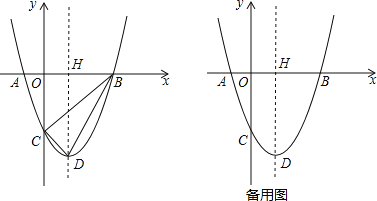
(1)求A,B两点的坐标;
(2)设点P在x轴下方的抛物线上,当∠ABP=∠CDB时,求出点P的坐标;
(3)以OB为边最第四象限内作等边△OBM.设点E为x轴的正半轴上一动点(OE>OH),连接ME,把线段ME绕点M顺时针旋转60°得MF,求线段DF的长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
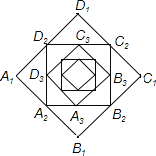
【题目】如图,小宋作出了边长为2的第一个正方形A1B1C1D1,算出了它的面积.然后分别取正方形A1B1C1D1四边的中点A2、B2、C2、D2作出了第二个正方形A2B2C2D2,算出了它的面积.用同样的方法,作出了第三个正方形A3B3C3D3,算出了它的面积…,由此可得,第六个正方形A6B6C6D6的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“石头、剪刀、布”是民间广为流传的游戏,游戏时,双方每次只能做“石头”、“剪刀”、“布”这三种手势中的一种.假定双方每次都是等可能的做这三种手势.
问:小强和小刚在一次游戏时,
(1)两个人同时出现“石头”手势的概率是多少?
(2)两个人出现不同手势的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y=![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com