解:(1)原式=(-1+3)+(-5+7)+(-9+11)+…+(-1997+1999)
=2×
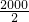
×

=1000;
(2)原式=(11-13)+(12-14)+(15-17)+…+(95-97)+(96-98)+(99+100)
=-2×
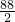
+199
=-88+199=111;
(3)原式=(1990+1)(2000-1)-1990×2000
=1990×2000-1990+2000-1-1990×2000
=10-1
=9;
(4)原式=472634
2+472635
2-(472634-1)×(472634+1)-(472635-1)(472635+1)
=472634
2+472635
2-472634
2+1-472635
2+1
=2;
(5)原式=

×(1-

+

-

+…+

-

)
=

×(1-

)
=

×
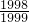
=

;
(6)根据题意可知第n项就是a
n=1+3(n-1),
即有244=1+3(n-1),
∴n=82,
∴一共有82个数,
又∵1+244=245,4+241=245…,
∴原式=(1+244)×82=20090;
(7)设原式=m,
那么3m=3+m-

,
∴2m=3-

,
∴m=

;
(8)原式=

-
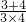
+

-

+

-

=(1+

)-(

+

)+(

+

)-(

+

)+(

+

)-(

+

)
=1+

-

-

+…-

-

=1-

=
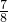
.
分析:(1)相邻两个数之和等于2,一共有
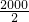
个数,再进行计算即可;
(2)每四个数之间有规律,地一个和第三个数之和等于-2,第二个数与第四个数之和等于-2,一共90个数,再计算即可;(3)把1991换成1990+1,1999换成2000-1计算即可;
(4)利用平方差公式计算即可;
(5)利用
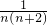
=

×(

-
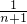
)计算即可;
(6)第一个数与最后一个数之和等于245,第二个数与倒数第二个数之和等于245,于是只要求出有几个数即可,最后一个数等于1+3(n-1),即可求出个数,再进行计算即可;
(7)设原式=m,则么3m=3+m-

,再解出m即可;
(8)先对原式变形,再利用

=

+
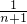
进行计算即可.
点评:本题考查的是有理数的运算能力,注意公式及规律的运用.

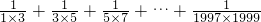
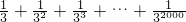
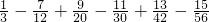 .
.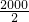 ×
×
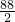 +199
+199 ×(1-
×(1- +
+ -
- +…+
+…+ -
- )
) ×(1-
×(1- )
) ×
×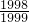
 ;
; ,
, ,
, ;
; -
-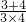 +
+ -
- +
+ -
-
 )-(
)-( +
+ )+(
)+( +
+ )-(
)-( +
+ )+(
)+( +
+ )-(
)-( +
+ )
) -
- -
- +…-
+…- -
-

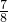 .
.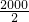 个数,再进行计算即可;
个数,再进行计算即可;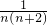 =
= ×(
×( -
-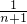 )计算即可;
)计算即可; ,再解出m即可;
,再解出m即可; =
= +
+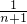 进行计算即可.
进行计算即可.
