
【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题: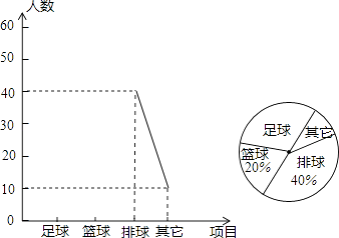
(1)在这次调查中,一共调查名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角度;
(3)将折线统计图补充完整.
【答案】
(1)100
(2)108
(3)解:爱好“足球”人数为:100×30%=30人,
爱好“篮球”人数为:100﹣30﹣40﹣10=20人,补全折线统计图如下:
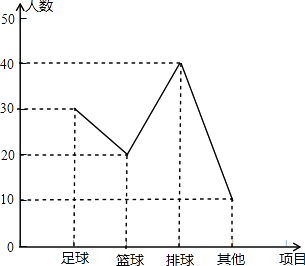
【解析】解:(1)根据题意,知爱好“排球”的有40人,占被调查人数的40%,
故被调查人数为:40÷40%=100(人);(2)“其他”项目占被调查人数百分比为: ![]() ×100%=10%,则“足球”项目人数占被调查人数的百分比为:1﹣(20%+40%+10%)=30%,
×100%=10%,则“足球”项目人数占被调查人数的百分比为:1﹣(20%+40%+10%)=30%,
则在扇形统计图中,“足球”所在扇形圆心角为:360°×30%=108°;
所以答案是:(1)100,(2)108.
【考点精析】关于本题考查的扇形统计图和折线统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比才能得出正确答案.


科目:初中数学 来源: 题型:
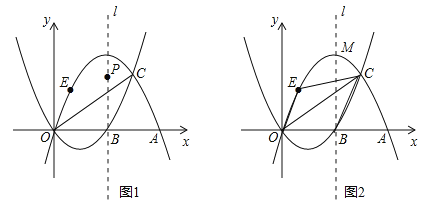
【题目】如图1,抛物线![]() :
:![]() 与
与![]() :
:![]() 相交于点O、C,
相交于点O、C,![]() 与
与![]() 分别交x轴于点B、A,且B为线段AO的中点.
分别交x轴于点B、A,且B为线段AO的中点.
(1)求![]() 的值;
的值;
(2)若OC⊥AC,求△OAC的面积;
(3)抛物线C2的对称轴为l,顶点为M,在(2)的条件下:
①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;
②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com