
【题目】△ABC中,AB=AC,D为BC的中点,以D为顶点作∠MDN=∠B,
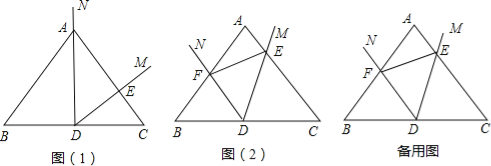
(1)如图(1)当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似的三角形.
(2)如图(2),将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于E,F点(点E与点A不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图(2)中,若AB=AC=10,BC=12,当△DEF的面积等于△ABC的面积的![]() 时,求线段EF的长.
时,求线段EF的长.
【答案】(1)△ABD,△ACD,△DCE(2)△BDF∽△CED∽△DEF,证明见解析;(3)5.
【解析】
(1)根据等腰三角形的性质以及相似三角形的判定得出△ADE∽△ABD∽△ACD∽△DCE,同理可得:△ADE∽△ACD.△ADE∽△DCE.
(2)利用已知首先求出∠BFD=∠CDE,即可得出△BDF∽△CED,再利用相似三角形的性质得出![]() ,从而得出△BDF∽△CED∽△DEF.
,从而得出△BDF∽△CED∽△DEF.
(3)利用△DEF的面积等于△ABC的面积的![]() ,求出DH的长,从而利用S△DEF的值求出EF即可
,求出DH的长,从而利用S△DEF的值求出EF即可
解:(1)图(1)中与△ADE相似的有△ABD,△ACD,△DCE.
(2)△BDF∽△CED∽△DEF,证明如下:
∵∠B+∠BDF+∠BFD=180°,∠EDF+∠BDF+∠CDE=180°,
又∵∠EDF=∠B,
∴∠BFD=∠CDE.
∵AB=AC,
∴∠B=∠C.
∴△BDF∽△CED.
∴![]() .
.
∵BD=CD,
∴![]() ,即
,即![]() .
.
又∵∠C=∠EDF,
∴△CED∽△DEF.
∴△BDF∽△CED∽△DEF.
(3)连接AD,过D点作DG⊥EF,DH⊥BF,垂足分别为G,H.
∵AB=AC,D是BC的中点,
∴AD⊥BC,BD=![]() BC=6.
BC=6.
在Rt△ABD中,AD2=AB2﹣BD2,即AD2=102﹣62,
∴AD=8.
∴S△ABC=![]() BCAD=
BCAD=![]() ×12×8=48,
×12×8=48,
S△DEF=![]() S△ABC=
S△ABC=![]() ×48=12.
×48=12.
又∵![]() ADBD=
ADBD=![]() ABDH,
ABDH,
∴![]() .
.
∵△BDF∽△DEF,
∴∠DFB=∠EFD.
∵DH⊥BF,DG⊥EF,
∴∠DHF=∠DGF.
又∵DF=DF,
∴△DHF≌△DGF(AAS).
∴DH=DG=![]() .
.
∵S△DEF=![]() ·EF·DG=
·EF·DG=![]() ·EF·
·EF·![]() =12,
=12,
∴EF=5.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形,定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为______;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.则△ACD与△ABC的相似比为_____;则△BCD与△ABC的相似比为_____;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a=_____(用含b的式子表示):
②如图3﹣2,若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a=______(用含n,b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
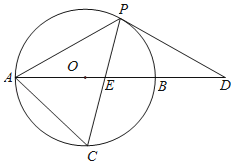
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=2,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA=BE,∠A=∠E,∠ABE=∠CBD,ED交BC于点F,且∠FBD=∠D.
求证:AC∥BD.
证明:∵∠ABE=∠CBD(已知),
∴∠ABE+∠EBC=∠CBD+∠EBC( )
即∠ABC=∠EBD
在△ABC和△EBD中,
 ,
,
∴△ABC≌△EBD( ),
∴∠C=∠D( )
∵∠FBD=∠D,
∴∠C= (等量代换),
∴AC∥BD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长是![]() 个单位长度,以点
个单位长度,以点![]() 为位似中心,在网格中画
为位似中心,在网格中画![]() ,使
,使![]() 与
与![]() 位似,且
位似,且![]() 与
与![]() 的位似比为
的位似比为![]() ,则点
,则点![]() 的坐标可以为( )
的坐标可以为( )
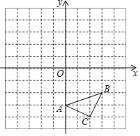
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).
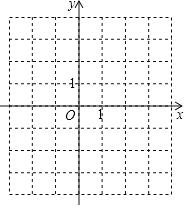
(1)求二次函数的解析式;
(2)在图中,画出二次函数的图象;
(3)根据图象,直接写出当y≤0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
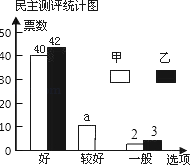
【题目】在校园歌手大赛中,甲、乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:(说明:随机抽取的50名同学每人必须从“好”、“较好”、“一般”中选一票投给每个选手)
A | B | C | D | E | F | |
甲 | 89 | 97 | 90 | 93 | 95 | 94 |
乙 | 89 | 92 | 90 | 97 | 94 | 94 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)学校规定评分标准如下:去掉评委评分中最高和最低分,再算平均分并将平均分与民意测评分按2:3计算最后得分.求甲、乙两位同学的最后得分.(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
查看答案和解析>>
科目:初中数学 来源: 题型:
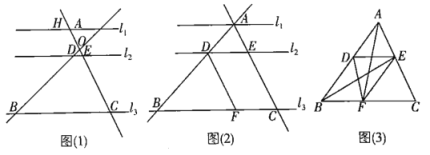
【题目】如图(1),![]() ,直线AB和CH交于点O,分别交
,直线AB和CH交于点O,分别交![]() 于D、E两点,已知
于D、E两点,已知![]() ,
,![]() ,
,![]() .
.
(1)尝试探究:在图(1)中,求DB和AD的长;
(2)类比延伸:平移AB使得A与H重合,如图(2)所示,过点D作![]() ,若
,若![]() ,求线段BF的长;
,求线段BF的长;
(3)拓展迁移:如图(3),若![]() 的面积是10,点D、E分别位于AB、CA上,
的面积是10,点D、E分别位于AB、CA上,![]() ,点F在BC上且
,点F在BC上且![]() ,
,![]() ,如果
,如果![]() 的面积和四边形FCED的面积相等,求这个相等的面积.
的面积和四边形FCED的面积相等,求这个相等的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com