
分析 (1)锐锐两次“求助”都在第一道题中使用,第一道肯定能对,第二道对的概率为$\frac{1}{4}$,即可得出结果;
(2)由题意得出第一道题对的概率为$\frac{1}{3}$,第二道题对的概率为$\frac{1}{2}$,即可得出结果;
(3)用树状图得出共有6种等可能的结果,锐锐顺利通关的只有1种情况,即可得出结果.
解答 解:(1)第一道肯定能对,第二道对的概率为$\frac{1}{4}$,
所以锐锐通关的概率为$\frac{1}{4}$;
故答案为:$\frac{1}{4}$;
(2)锐锐两次“求助”都在第二道题中使用,
则第一道题对的概率为$\frac{1}{3}$,第二道题对的概率为$\frac{1}{2}$,
所以锐锐能通关的概率为$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{6}$;
故答案为:$\frac{1}{6}$;
(3)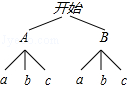 锐锐将每道题各用一次“求助”,分别用A,B表示剩下的第一道单选题的2个选项,a,b,c表示剩下的第二道单选题的3个选项,
锐锐将每道题各用一次“求助”,分别用A,B表示剩下的第一道单选题的2个选项,a,b,c表示剩下的第二道单选题的3个选项,
树状图如图所示:
共有6种等可能的结果,锐锐顺利通关的只有1种情况,
∴锐锐顺利通关的概率为:$\frac{1}{6}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届浙江省平阳县名校九年级下学期第一次模拟统练数学试卷(解析版) 题型:判断题
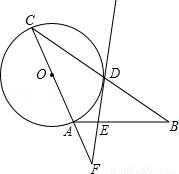
(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,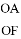 =
= 时,求DE的长.
时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a-b)(2a+b) | B. | (x+2y)(-2y+x) | C. | (2a+b)(a-2b) | D. | (-x-y)(-x+y) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com