
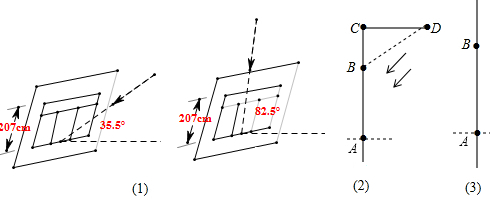
分析 (1)根据题意结合入射角度进而画出符合题意的图形即可;
(2)首先设CD=x,则tan35.5°=$\frac{BC}{CD}$,表示出BC的长,进而利用tan82.5°=$\frac{AC}{CD}$求出DC的长,进而得出答案.
解答 解:(1)如图所示: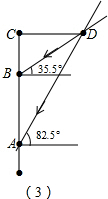
(2)由题意可得出:∠CDB=35.5°,∠CDA=82.5°,
设CD=x,则tan35.5°=$\frac{BC}{CD}$,
∴BC=0.71x,
∴在Rt△ACD中,
tan82.5°=$\frac{AC}{CD}$=$\frac{207+0.71x}{x}$=7.6,
解得:x≈30,
∴BC=0.71×30≈21(cm),
答:BC的长度是21cm,CD的长度是30cm.
点评 此题主要考查了解直角三角形的应用,正确选择锐角三角函数关系进而求出CD的长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
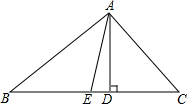 已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,
已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
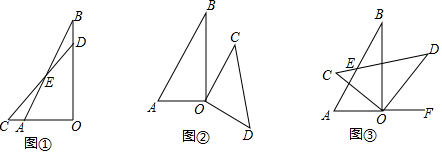
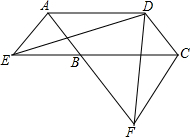 如图,已知:?ABCD中,∠ABC=120°,分别延长AB,CB到点F,E,使得△BCF和△ABE都是等边三角形,连接DE,DF.
如图,已知:?ABCD中,∠ABC=120°,分别延长AB,CB到点F,E,使得△BCF和△ABE都是等边三角形,连接DE,DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com