
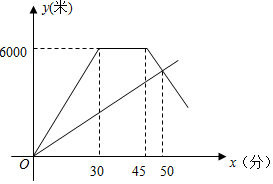
 甲乙两地相距6000米,李军和王伟同时从甲地出发匀速前往乙地,李军到达乙地后休息一段时间后,以原来的速度从原路返回,如图所示是两人离甲地的距离y(米)与出发时间x(分)之间的函数图象.
甲乙两地相距6000米,李军和王伟同时从甲地出发匀速前往乙地,李军到达乙地后休息一段时间后,以原来的速度从原路返回,如图所示是两人离甲地的距离y(米)与出发时间x(分)之间的函数图象.分析 (1)根据函数图象和题意可以求得李军的速度和到达乙地休息的时间;
(2)根据(1)中李军的速度可以求得两人相遇时李军离乙地的距离;
(3)根据图象中的数据和(2)中的答案可以求得王伟的速度,从而可以求得王伟到达乙地用的时间和李军返回甲地时的时间,然后比较大小即可解答本题.
解答 解:(1)由题意可得,
李军的速度为:6000÷30=200米/分,到达乙地后休息的时间为:45-30=15(分钟),
故答案为:200,15;
(2)由题意可得,
两人相遇时,李军离乙地的距离是:200×(50-45)=1000(米),
即两人相遇时,李军离乙地的距离是1000米;
(3)当李军返回到甲地时,王伟到达乙地,
理由:王伟的速度是:(6000-1000)÷50=100米/分,
则王伟到达乙地用的时间为:6000÷100=60(分钟),
李军返回甲地时的时间为:45+30=75(分钟),
∵60<75,
∴当李军返回到甲地时,王伟到达乙地.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的思想和数形结合的思想解答.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
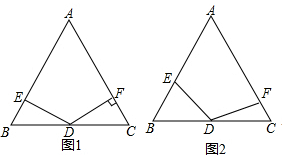
 如图,有下列判断①∠1与∠3是对顶角②∠1与∠4是内错角③∠1与∠2是同旁内角④∠3与∠4是同位角,其中不正确的是( )
如图,有下列判断①∠1与∠3是对顶角②∠1与∠4是内错角③∠1与∠2是同旁内角④∠3与∠4是同位角,其中不正确的是( )| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
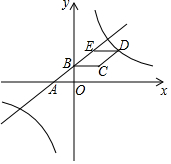 如图,在平面直角坐标系中,菱形BCDE的一边BC平行于x轴,点D在第一象限,直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,并经过点E,且点B是AE的中点,店D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,在平面直角坐标系中,菱形BCDE的一边BC平行于x轴,点D在第一象限,直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,并经过点E,且点B是AE的中点,店D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com