
【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:

并求得了A产品三次单价的平均数和方差:
![]() ;
; ![]()
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的平均数和方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,若B产品第四次调价后为m元(3<m<4),此时B产品四次单价的中位数是A产品这四次单价的中位数的![]() 倍,求m.
倍,求m.

【答案】(1)25;(2)3.5, ![]() ,B产品的单价波动小;(3) a的值是6.2元/件.
,B产品的单价波动小;(3) a的值是6.2元/件.
【解析】试题分析:(1)根据题目提供数据补充折线统计图即可;
(2)分别计算平均数及方差即可;
(3)首先确定B产品第四次调价的单价,然后确定B产品这四次单价的中位数,然后确定A产品这四次单价的中位数,再列式求a即可.
试题解析:解:(1)如图2所示:
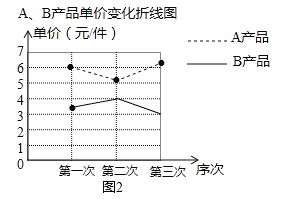
B产品第三次的单价比上一次的单价降低了![]() =25%;
=25%;
(2)![]() =
=![]() ×(3.5+4+3)=3.5,
×(3.5+4+3)=3.5, ![]() =
=![]() =
=![]() ,∵B产品的方差小,∴B产品的单价波动小;
,∵B产品的方差小,∴B产品的单价波动小;
(3)第四次单价为3×(1+20%)=3.6(元/件),第四次调价后,对于B产品,这四次单价的中位数为=![]() =3.55(元/件),3.55×2﹣1=6.1(元/件),a=6.1×2﹣6=6.2(元/件).
=3.55(元/件),3.55×2﹣1=6.1(元/件),a=6.1×2﹣6=6.2(元/件).
故a的值是6.2元/件.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某超市账目记录显示,第一天卖出39支牙刷和21盒牙膏,收入300元;第二天以同样的价格卖出同样的52支牙刷和28盒牙膏,收入应该是____________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表为深圳市居民每月用水收费标准,(单位:元/m3).
用水量 | 单价 |
x≤22 | a |
剩余部分 | a+1.1 |
(1)某用户用水10立方米,共交水费23元,求a的值;
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)

(1)如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.
求证:△ABF≌△DAE;
(2)直接写出(1)中,线段EF与AF、BF的等量关系 ;
(3)①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E,则图中全等三角形是 ,线段EF与AF、BF的等量关系是 ;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,线段EF与AF、BF的等量关系是 ;
(4)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图、探究线段EF与AF、BF的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c的图象交x轴于点A(﹣4,0)和点B,交y轴于点C(0,4).
(1)求这个二次函数的表达式;
(2)在抛物线的对称轴上是否存在一点P,使得![]() 的值最大?若存在,求出P点坐标;若不存在,请说明理由.
的值最大?若存在,求出P点坐标;若不存在,请说明理由.
(3)在平面直角坐标系内,是否存在点Q,使A,B,C,Q四点构成平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
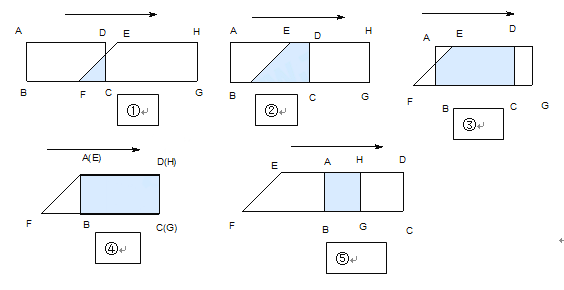
【题目】已知:如图,在矩形ABCD中,AD=6㎝,AB=3㎝。在直角梯形中EFGH中 ,EH∥FG ,∠EFG=![]() ,∠G=
,∠G=![]() ,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移,
,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移, ![]() 秒后,矩形ABCD与梯形EFGH重合部分的面积为
秒后,矩形ABCD与梯形EFGH重合部分的面积为![]() ㎝。按要求回答下列各题(不要求写出解题过程):
㎝。按要求回答下列各题(不要求写出解题过程):
(1)当![]() 时,
时, ![]() cm2(如图①);
cm2(如图①);
当![]() 时,
时, ![]() cm2(如图④);
cm2(如图④);
(2)在下列各种情况下,分别用![]() 表示
表示![]() :
:
如图①,当![]() 时,
时, ![]() cm2;
cm2;
如图②,当![]() 时,
时, ![]() cm2;
cm2;
如图③,当![]() 时,
时, ![]() cm2;
cm2;
如图⑤,当![]() 时,
时, ![]() cm2.
cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com