
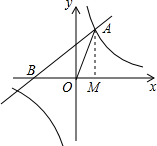
 已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).
已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).分析 (1)把点A(1,n)坐标代入$y=\frac{{\sqrt{3}}}{x}$即可求得n,再把$A(1,\sqrt{3})$坐标代入$y=\frac{{\sqrt{3}}}{3}x+m$可求m;
(2)由直线$y=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$,求得点B的坐标为(-2,0),即OB=2,由点A的坐标为$(1,\sqrt{3})$,由三角函数可求得∠AOM=60°,由勾股定理求得得 OA=2,得到OA=OB,推出∠OBA=∠BAO,于是求得∠BAO=30°,由正弦函数的定义可得结论.
解答 解:(1)∵点A(1,n)在双曲线$y=\frac{{\sqrt{3}}}{x}$上,
∴n=$\sqrt{3}$,
又∵A(1,$\sqrt{3}$)在直线y=$\frac{\sqrt{3}}{3}$x+m上,
∴m=$\frac{2\sqrt{3}}{3}$;
(2)过点A作AM⊥x轴于点M.
∵直线$y=\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$与x轴交于点B,
∴$\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}=0$.
解得 x=-2.
∴点B的坐标为(-2,0).
∴OB=2,
∵点A的坐标为$(1,\sqrt{3})$,
∴AM=$\sqrt{3}$,OM=1,
在Rt△AOM中,∠AMO=90°,
∴tan$∠AOM=\frac{AM}{OM}=\sqrt{3}$,
∴∠AOM=60°,
由勾股定理,得 OA=2,
∴OA=OB,
∴∠OBA=∠BAO,
∴∠BAO=$\frac{1}{2}∠$AOM=30°,
∴sin∠BAO=$\frac{1}{2}$,
∴∠BA0=30°.
点评 本题考查了反比例函数与一次函数的交点,三角函数的定义,利用点的坐标得到∠BAO的度数是解决本题的突破点.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
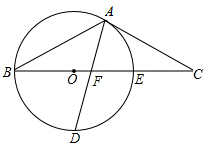 如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.
如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
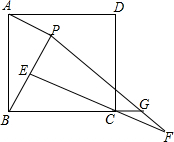 如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.
如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.518×107元 | B. | 5.18×106元 | C. | 51.8×105元 | D. | 518×104元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
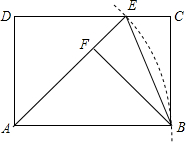 如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.
如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com