
.把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
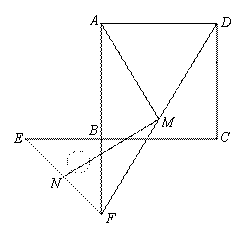 (2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.

图1 图2
(1)解:连接DE,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠DAB=∠DCE=90°,
∵点M是DF的中点,
∴AM= DF.
DF.
∵△BEF是等腰直角三角形,
∴AF=CE,
在△ADF与△CDE中,
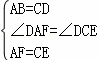 ,
,
∴△ADF≌△CDE(SAS),
∴DE=DF.
∵点M,N分别为DF,EF的中点,
∴MN是△EFD的中位线,
∴MN= DE,
DE,
∴AM=MN;
∵MN是△EFD的中位线,
∴MN∥DE,
∴∠FMN=∠FDE.
∵AM=MD,
∴∠MAD=∠ADM,
∵∠AMF是△ADM的中位线,
∴∠AMF=2∠ADM.
∵△ADF≌△CDE,
∴∠ADM=∠DEC,
∴∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,
∴MA⊥MN.
∴MA=MN,MA⊥MN.
(2)成立.
理由:连接DE.
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.
在Rt△ADF中,
∵点M是DF的中点,
∴MA= DF=MD=MF,
DF=MD=MF,
∴∠1=∠3.
∵点N是EF的中点,
∴MN是△DEF的中位线,
∴MN= DE,MN∥DE.
DE,MN∥DE.
∵△BEF是等腰直角三角形,
∴BF=BF,∠EBF=90°.
∵点E、F分别在正方形CB、AB的延长线上,
∴AB+BF=CB+BE,即AF=CE.
在△ADF与△CDE中,
∵
∴△ADF≌△CDE,
∴DF=DE,∠1=∠2,
∴MA=MN,∠2=∠3.
∵∠2+∠4=∠ABC=90°,∠4=∠5,
∴∠3+∠5=90°,
∴∠6=180°﹣(∠3+∠5)=90°,
∴∠7=∠6=90°,MA⊥MN.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
3个旅游团游客年龄的方差分别是: =1.4,
=1.4, =18.8,
=18.8, =2.5,导游小方喜欢带游客
=2.5,导游小方喜欢带游客
年龄相近的团队,则他应该选择 ( )
A.甲团 B.乙团 C.丙团 D.哪一个都可以
查看答案和解析>>
科目:初中数学 来源: 题型:
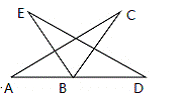
如图,△ABC绕点B顺时针旋转到△EBD位置,若∠A=30°,∠D=15°,A,B,D在同一直线上,则旋转的角度是()
A. 50° B . 45° C. 40° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com