
 在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移3个单位称为1次变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是(14,-1-$\sqrt{3}$).
在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移3个单位称为1次变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是(14,-1-$\sqrt{3}$). 分析 首先由△ABC是等边三角形,点B、C的坐标分别是(-1,-1)、(-3,-1),求得点A的坐标,然后根据题意求得第1次、2次、3次变换后的点A的对应点的坐标,即可得规律:第n次变换后的点A的对应点的为:当n为奇数时为(2n-2,1+$\sqrt{3}$),当n为偶数时为(2n-2,-1-$\sqrt{3}$),继而求得把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标.
解答 解:∵△ABC是等边三角形,点B、C的坐标分别是(-1,-1)、(-3,-1),
∴点A的坐标为(-2,-1-$\sqrt{3}$),
根据题意得:第1次变换后的点A的对应点的坐标为(-2+2,1+$\sqrt{3}$),即(0,1+$\sqrt{3}$),
第2次变换后的点A的对应点的坐标为(0+2,-1-$\sqrt{3}$),即(2,-1-$\sqrt{3}$),
第3次变换后的点A的对应点的坐标为(2+2,1+$\sqrt{3}$),即(4,1+$\sqrt{3}$),
第n次变换后的点A的对应点的为:当n为奇数时为(2n-2,1+$\sqrt{3}$),当n为偶数时为(2n-2,-1-$\sqrt{3}$),
∴把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是:(14,-1-$\sqrt{3}$).
故答案为:(14,-1-$\sqrt{3}$).
点评 此题考查了对称与平移的性质.此题难度较大,属于规律性题目,注意得到规律:第n次变换后的点A的对应点的为:当n为奇数时为(2n-2,1+$\sqrt{3}$),当n为偶数时为(2n-2,-1-$\sqrt{3}$)是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
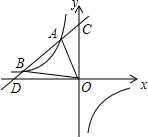 如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.
如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
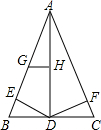 如图,已知AB=AC,AD是中线,BE=CF.
如图,已知AB=AC,AD是中线,BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
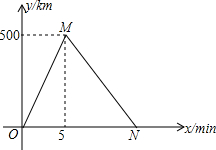 小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.
小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.
如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com