
(2006山西课改,26)(14分)如图,已知抛物线 与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).

(1)求抛物线 关于原点对称的抛物线
关于原点对称的抛物线 的解析式;
的解析式;
(2)设抛物线 的顶点为M,抛物线
的顶点为M,抛物线 与x轴分别交于C、D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
与x轴分别交于C、D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值;
(4)在运动过程中,四边形MDNA能否形成矩形?若能,求出此时t的值;若不能,请说明理由.
|
(1)点A(-4,0),点B(-2,0),点E(0,8) 关于原点的对称点分别为 D(4,0),C(2,0),F(0,-8).设抛物线 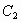 的解析式是 的解析式是
则 所以所求抛物线的解析式是 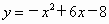 . .
(2)由(1)可计算得点M(-3,-1),N(3,1) 过点 N作NH⊥AD,垂足为H.当运动到时刻 t时,AD=2OD=8-2t,NH=1+2t.根据中心对称的性质 OA=OD,OM=ON,所以四边形MDNA是平行四边形.所以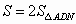 . .
所以,四边形 MDNA的面积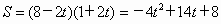 . .
因为运动至点 A与点D重合为止,据题意可知0≤t<4.所以,所求关系式是 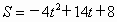 ,t的取值范围是0≤t<4. ,t的取值范围是0≤t<4.
(3) 所以 (4)在运动过程中四边形MDNA能形成矩形. 由(2)知四边形MDNA是平行四边形,对角线是AD、MN,所以当AD=MN,时四边形MDNA是矩形. 所以OD=ON.所以 所以 所以在运动过程中四边形MDNA可以形成矩形,此时 |
|
也可用顶点坐标公式来求. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:022
(2006山西课改,7)北京与纽约的时差为-13(负号表示同一时刻纽约时间比北京时间晚).如果现在是北京时间15∶00,那么纽约时间是________.
查看答案和解析>>
科目:初中数学 来源: 题型:022
(2006山西课改,10)如图,在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连结ED并延长到点F,使DF=DE,连结FC,若∠B=70°,则∠F=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:044
(2006山西课改,21)课堂上,李老师给大家出了这样一道题:当x=3,5- ,7+
,7+ 时,求代数式
时,求代数式 ÷
÷ 的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
查看答案和解析>>
科目:初中数学 来源: 题型:022
(2006山西课改,4)如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻.当他带球冲到A点时,同样乙已经助攻冲到B点.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门,仅从射门角度考虑,应选择________种射门方式.

查看答案和解析>>
科目:初中数学 来源: 题型:044
(2006山西课改,23)下表是我国近几年的进口额与出口额数据(近似值)统计表:

(1)下图是描述这两组数据的折线图,请你将进口额折线图补充完整;
 (2)计算2000年至2002年出口额年平均增长率(
(2)计算2000年至2002年出口额年平均增长率( );
);
(3)观察折线图,你还能得到什么信息,写出两条.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com